




Next: Data Variability
Up: REVIEW
Previous: REVIEW
What we choose for 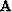 can have a significant
affect on our model estimate.
In theory
can have a significant
affect on our model estimate.
In theory 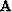 should be a matrix of size nm by nm (where
nm is the number of model elements).
People use numerous approximations for
should be a matrix of size nm by nm (where
nm is the number of model elements).
People use numerous approximations for 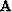 .Some of the more common
.Some of the more common
The first option makes the assumption that our model is
smooth and stationary. The second option still assumes
stationarity, but allows for much more sophisticated covariance
descriptions.
The third option allows for non-stationarity but is only valid
when a model has a single dip at each location and requires
some a priori knowledge about the model. The last
is the best representation of the inverse model covariance
matrix. Unfortunately, it requires a field with the same
properties as the model in order to be constructed. In addition, it
faces stability problems Rickett (2001).
At least the first three methods, and possibly all four (depending
on the field we use and the filter description we choose to estimate the NSPEF)
are limited to describing second order statistics.
In addition we normally try to describe the inverse
covariance through a filter with only a few coefficients.
In terms of the covariance matrix, we are putting non-zero coefficients
along only a few diagonals.
Finally,/ all of these approaches assume that the main diagonal of the
inverse covariance matrix is a constant.
The problems with these approximations are demonstrated in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The left panel shows measurements of the sea depth for a day.
A PEF is estimated at the known locations and used as
.
The left panel shows measurements of the sea depth for a day.
A PEF is estimated at the known locations and used as 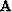 with fitting goals,
with fitting goals,
|  |
(6) |
| |
where 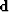 is shown in the left panel of Figure
is shown in the left panel of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and
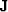 is a selector matrix (1 at known locations, 0 at unknown).
The center panel of Figure
is a selector matrix (1 at known locations, 0 at unknown).
The center panel of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the estimated model.
Note how the estimated portion of the model doesn't have the right
texture. The variance of the model is not the same as the
variance of the data.
This is due to the combination of two factors.
seabeam
shows the estimated model.
Note how the estimated portion of the model doesn't have the right
texture. The variance of the model is not the same as the
variance of the data.
This is due to the combination of two factors.
seabeam
Figure 1 The left panel shows the result of recording the sea depth for one day.
The center panel shows the interpolation result using a filter
estimated from the known portion of the data and then solving (6).
Note the difference in variance in the known and unknown portions of
the model. The right panel is the filter response of the PEF used
for interpolation.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





- Our covariance description has a limited range. The right
panel of Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show the result
of applying the inverse PEF (or more correctly
show the result
of applying the inverse PEF (or more correctly
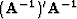 ) to a spike in the center of the model.
Note how the response tends towards zero.
) to a spike in the center of the model.
Note how the response tends towards zero.
- Our inverse problem will give us a minimum energy
solution, which means it is going to want to fill the residual vectors
with as small numbers as possible.
In previous papers Clapp (2000, 2001a), I showed
how we can change what the minimum energy solution will be
by introducing an initial condition to our residual vector filled
with random numbers.
In terms of our fitting goals (6) we are replacing
the zero vector of our model styling fitting goal with
with standard normal noise vector 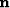 , scaled by some
scalar
, scaled by some
scalar 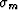 ,
,
|  |
(7) |
| |
For the special case of missing data problems, where 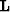 is
simply a masking operator
is
simply a masking operator 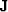 delineating
known and unknown points, Claerbout (1999) showed how
delineating
known and unknown points, Claerbout (1999) showed how 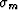 can
be approximated by first estimating the
model through the fitting goals in (6), then by solving
can
be approximated by first estimating the
model through the fitting goals in (6), then by solving
| 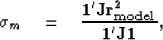 |
(8) |
where 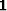 is a vector composed of 1s.
Figure
is a vector composed of 1s.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the model using three
different
shows the model using three
different 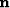 vectors. Note how the variance
of the model is now similar to the variance of the data.
A good check of this is whether the original recording
path can be seen.
seabeam2
vectors. Note how the variance
of the model is now similar to the variance of the data.
A good check of this is whether the original recording
path can be seen.
seabeam2
Figure 2 Three realizations of the interpolation problem using
fitting goals (8).
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





Using equation (8) to estimate
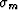 makes the assumption that
our covariance description is correct. When our
assumptions on stationarity are incorrect or filter shape
is insufficient to correctly describe the covariance,
this approach will be ineffective.
makes the assumption that
our covariance description is correct. When our
assumptions on stationarity are incorrect or filter shape
is insufficient to correctly describe the covariance,
this approach will be ineffective.





Next: Data Variability
Up: REVIEW
Previous: REVIEW
Stanford Exploration Project
7/8/2003
![]() can have a significant
affect on our model estimate.
In theory
can have a significant
affect on our model estimate.
In theory ![]() should be a matrix of size nm by nm (where
nm is the number of model elements).
People use numerous approximations for
should be a matrix of size nm by nm (where
nm is the number of model elements).
People use numerous approximations for ![]() .Some of the more common
.Some of the more common
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The left panel shows measurements of the sea depth for a day.
A PEF is estimated at the known locations and used as
.
The left panel shows measurements of the sea depth for a day.
A PEF is estimated at the known locations and used as ![]() with fitting goals,
with fitting goals,
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the estimated model.
Note how the estimated portion of the model doesn't have the right
texture. The variance of the model is not the same as the
variance of the data.
This is due to the combination of two factors.
shows the estimated model.
Note how the estimated portion of the model doesn't have the right
texture. The variance of the model is not the same as the
variance of the data.
This is due to the combination of two factors.

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show the result
of applying the inverse PEF (or more correctly
show the result
of applying the inverse PEF (or more correctly
![]() , scaled by some
scalar
, scaled by some
scalar ![]() ,
,
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the model using three
different
shows the model using three
different 
![]() makes the assumption that
our covariance description is correct. When our
assumptions on stationarity are incorrect or filter shape
is insufficient to correctly describe the covariance,
this approach will be ineffective.
makes the assumption that
our covariance description is correct. When our
assumptions on stationarity are incorrect or filter shape
is insufficient to correctly describe the covariance,
this approach will be ineffective.