Next: Example 3: Gulf of
Up: Haines et al.: Multiple
Previous: Example 1: A simple
We next apply non-stationary PEF's to the synthetic dataset described by
Sava and Guitton (2003). The model is designed to resemble a
typical Gulf of Mexico subsalt problem.
Each angle gather is processed separately, but the same parameters are
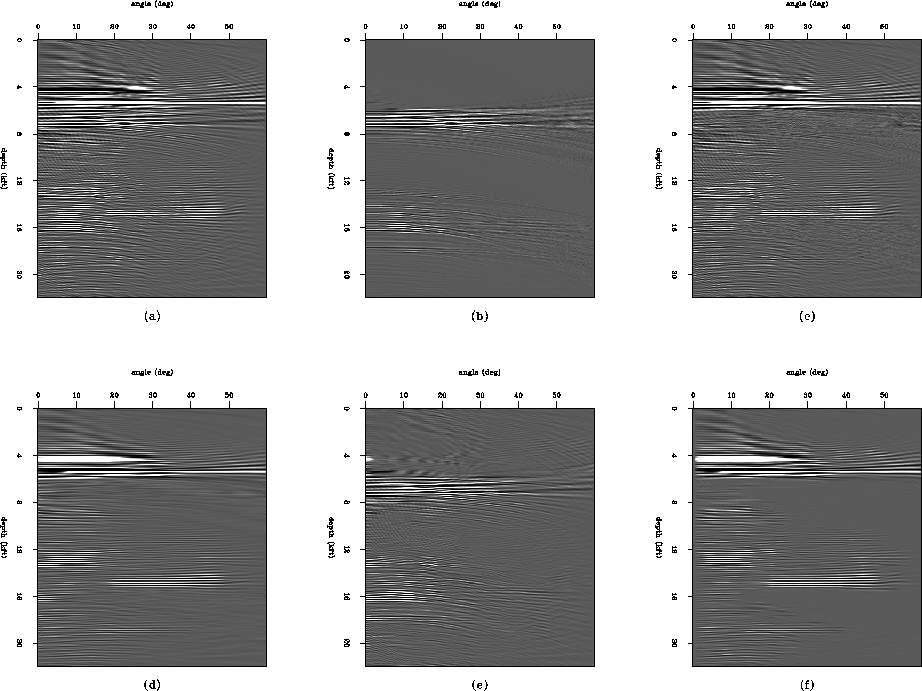
used for all gathers. A typical gather is shown in
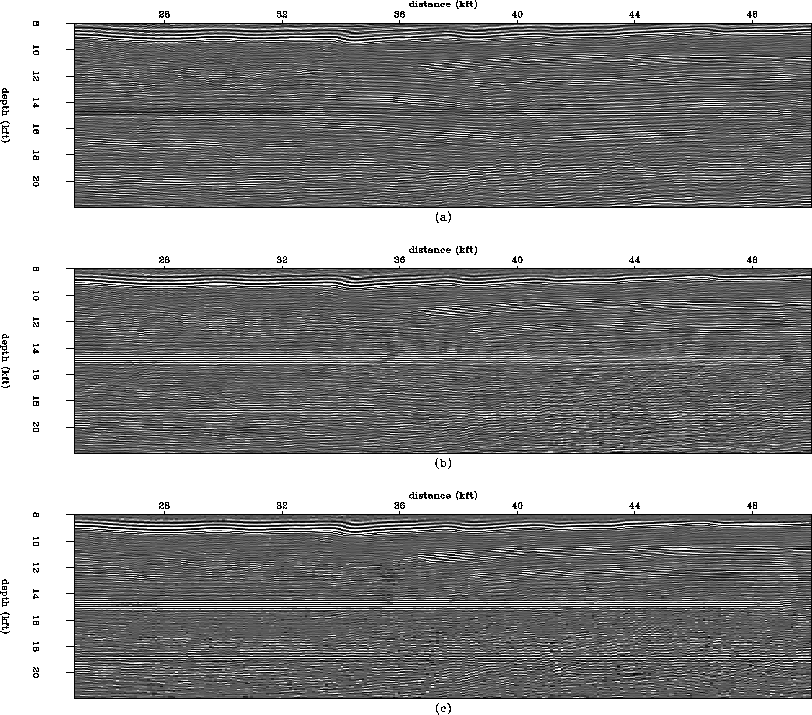
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a. For the noise PEF estimation we again
use the multiple
model estimated with the PRT approach (Figure
a. For the noise PEF estimation we again
use the multiple
model estimated with the PRT approach (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b), and for the signal PEF we use a
laterally smoothed version (Figure
b), and for the signal PEF we use a
laterally smoothed version (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) d) of the primary model
estimated from the PRT approach (Figure
d) of the primary model
estimated from the PRT approach (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c). The smoothing
is accomplished by averaging across 8 traces in each direction from a
given trace, and helps to weaken or remove the remaining multiple
energy. This improves the ability of the signal PEF's to accurately
represent the pattern of the signal. The primary model estimated by
the PEF approach is shown in Figure
c). The smoothing
is accomplished by averaging across 8 traces in each direction from a
given trace, and helps to weaken or remove the remaining multiple
energy. This improves the ability of the signal PEF's to accurately
represent the pattern of the signal. The primary model estimated by
the PEF approach is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) f, with the
corresponding multiple model in Figure
f, with the
corresponding multiple model in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) e. The result is
clearly a much better separation of the multiples from the primaries
in the angle domain.
e. The result is
clearly a much better separation of the multiples from the primaries
in the angle domain.
CIG_BP_nice
Figure 2 (a) Input data- one angle
gather from the synthetic. (b) Multiple model estimated with PRT approach. (c) Primary
model estimated from PRT approach. (d) Signal model used for PEF
estimation (smoothed version of (c)). (e) Multiple model estimated with PEF approach. (f)
Primary model estimated with PEF approach.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





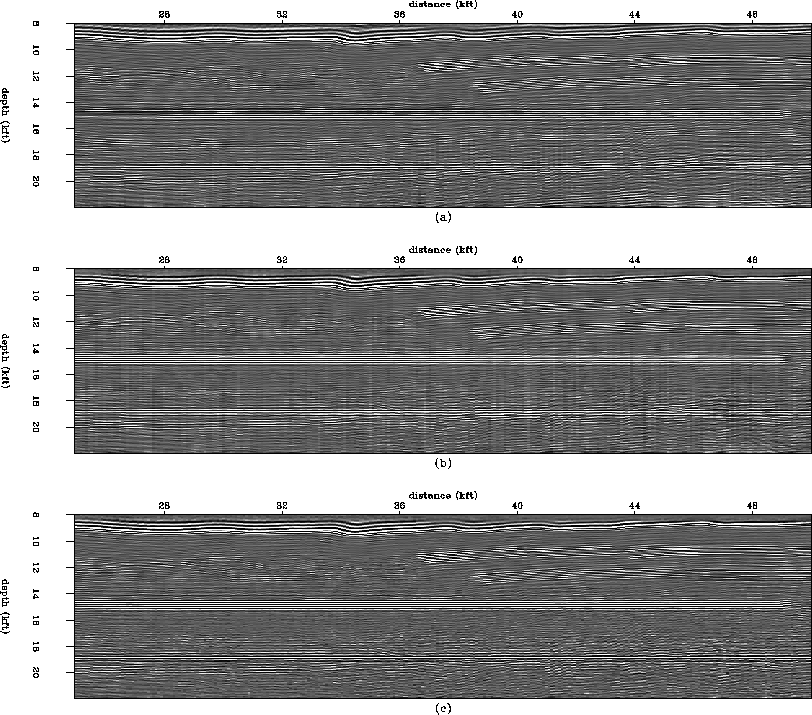
A comparison of common-angle gathers (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
highlights the effectiveness of the non-stationary PEF approach.
Figure
)
highlights the effectiveness of the non-stationary PEF approach.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a shows a window of the raw data at an angle of 15
degrees. Figure
a shows a window of the raw data at an angle of 15
degrees. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b shows the corresponding PRT
result, with improved resolution of the deeper reflectors. And Figure
b shows the corresponding PRT
result, with improved resolution of the deeper reflectors. And Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c shows the PEF result, with considerable improvement
over the PRT result, particularly of the reflector at 19 kft.
c shows the PEF result, with considerable improvement
over the PRT result, particularly of the reflector at 19 kft.
BP_CA
Figure 3 Common-angle gathers, at an
angle of 15 degrees. (a) Raw data. (b) PRT result. (c) PEF result,
with improved clarity of reflectors at 15 kft and 19 kft.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





The real test of effectiveness, of course, is a comparison of the stacked
results. A final stack of the raw data is shown in Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a, the PRT result in Figure
a, the PRT result in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b, and the final PEF
stack is shown in Figure
b, and the final PEF
stack is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c. The PEF result shows
improvement in the clarity of reflectors in the lower part of
the record.
c. The PEF result shows
improvement in the clarity of reflectors in the lower part of
the record.
BP_stack
Figure 4 Stacked images. (a) Stack
of raw data. (b) Stack of PRT result. (c) Stack of PEF result. Note
improved clarity of reflector at depth of 19 kft.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





We chose the smoothed PRT result as the model for estimation of the
signal PEF after testing several options. The PRT primary model
contains sufficient multiple energy that the PEF estimation is
impacted significantly, and the final estimated signal contains
considerable multiple energy as well. The use of  presents similar limitations and similar problems with the final
result, due to the inability of the noise PEF
presents similar limitations and similar problems with the final
result, due to the inability of the noise PEF  to
completely remove the multiple energy. The smoothed version of the
PRT primary model is the most effective model that we tested. The
smoothing helps to remove a considerable amount of the remaining
multiple energy and generally cleans up the model so that the PEF
estimation is a simpler problem. This smoothing would not be a wise
choice as a processing step on raw data, but it is acceptable
for cleaning up the PEF-estimation model and results in PEF's that are
well-suited to task of separating primaries from multiples in this case.
to
completely remove the multiple energy. The smoothed version of the
PRT primary model is the most effective model that we tested. The
smoothing helps to remove a considerable amount of the remaining
multiple energy and generally cleans up the model so that the PEF
estimation is a simpler problem. This smoothing would not be a wise
choice as a processing step on raw data, but it is acceptable
for cleaning up the PEF-estimation model and results in PEF's that are
well-suited to task of separating primaries from multiples in this case.





Next: Example 3: Gulf of
Up: Haines et al.: Multiple
Previous: Example 1: A simple
Stanford Exploration Project
7/8/2003
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a. For the noise PEF estimation we again
use the multiple
model estimated with the PRT approach (Figure
a. For the noise PEF estimation we again
use the multiple
model estimated with the PRT approach (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b), and for the signal PEF we use a
laterally smoothed version (Figure
b), and for the signal PEF we use a
laterally smoothed version (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) d) of the primary model
estimated from the PRT approach (Figure
d) of the primary model
estimated from the PRT approach (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) c). The smoothing
is accomplished by averaging across 8 traces in each direction from a
given trace, and helps to weaken or remove the remaining multiple
energy. This improves the ability of the signal PEF's to accurately
represent the pattern of the signal. The primary model estimated by
the PEF approach is shown in Figure
c). The smoothing
is accomplished by averaging across 8 traces in each direction from a
given trace, and helps to weaken or remove the remaining multiple
energy. This improves the ability of the signal PEF's to accurately
represent the pattern of the signal. The primary model estimated by
the PEF approach is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) f, with the
corresponding multiple model in Figure
f, with the
corresponding multiple model in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) e. The result is
clearly a much better separation of the multiples from the primaries
in the angle domain.
e. The result is
clearly a much better separation of the multiples from the primaries
in the angle domain.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)