Full prestack migration

In the previous section we have presented the simple common-azimuth case. We examine here how to extend the common-azimuth case to the full prestack case. There are two main differences. First, the rays may not be coplanar anymore along the travel path from the surface to the reflection point because of a cross-line offset due to ray bending Biondi (2001). If the migration velocity is correct, though, the two rays meets at the reflection point where they must be coplanar. Second, the non-coplanarity of the rays during the propagation induces the azimuth of the reflection to be different from the in-line direction.

The coplanarity is imposed at the reflection point by the coplanarity condition introduced by Biondi and Palacharla (1996). Some algebraic manipulations presented in annexe B allow us to write the coplanarity condition as  

$$k_{h_y}=\frac{k_{m_y}k_{m_x}k_{h_x}}{k_z^2+k_{m_y}^2},$$ (3)

where k_mx and k_my are the two components of the midpoint wavenumber, and k_hx and k_hy are the two components of the offset wavenumber.

The non-zero reflection azimuth issue is addressed by doing a local change of coordinates such as the azimuth is zero in the new coordinates system. If $\beta$ is the azimuth of the reflection in the original coordinates system (x,z), a rotation by an angle $\beta$ makes the reflection azimuth to be parallel to the new in-line direction in the new coordinates system (x',y') (cf. Figure ). In the new coordinates system, the midpoint wavenumber $\bf k'_m$and the offest wavenumber $\bf k'_h$ are defined by:

$$\begin{eqnarray} {\bf k'_m}&=& \left[ \begin{array} {c} {k'_{m_x}}\\ {k'_{m_y}... ...}} \\ \sin \beta k_{m_x} + \cos \beta {k_{m_y}}\end{array}\right]\end{eqnarray}$$ (4)

$$\begin{eqnarray} {\bf k'_h}&=& \left[ \begin{array} {c} {k'_{h_x}}\\ {k'_{h_y}... ...}} \\ \sin \beta k_{h_x} + \cos \beta {k_{h_y}}\end{array}\right]\end{eqnarray}$$ (5)

With these transformations, equations (2) and (3) can be rewritten for a non-zero azimuth of the reflection:

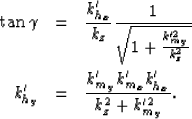$$\begin{eqnarray} \tan \gamma &=& \frac{k_{h_x}'}{k_z} \frac{1}{\sqrt{1+\frac{k_... ...} &=& \frac{ k_{m_y}' k'_{m_x} k'_{h_x} } { k_z^2 + k_{m_y}'^2 }.\end{eqnarray}$$ (6) (7)

 

rotation_beta Figure 4 The source-receiver axis is in the x' direction. Axis x' is the image of axis x after a rotation by 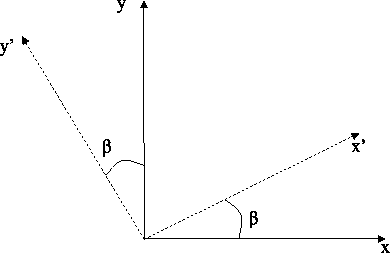$\beta$.In the new basis, the reflection has zero azimuth.