




Next: APPLYING THE OPERATORS TO
Up: CALCULATING THE OPERATORS
Previous: Derivatives of surface horizontal
Now that we can calculate the partial derivatives of traveltimes
and surface horizontal slownesses, the next step is to solve
equation (4) with proper initial conditions.
Let us take the residual depth migration of post-stack images as
an example. Assume that calculations are done in polar coordinates.
The initial conditions at the surface are
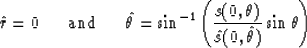
where 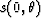 and
and 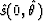 are slowness at the
shot-receiver
position. From these initial conditions we can extrapolate the
kinematic operators of residual depth migration in the radius direction
as follows:
are slowness at the
shot-receiver
position. From these initial conditions we can extrapolate the
kinematic operators of residual depth migration in the radius direction
as follows:
| ![\begin{displaymath}
\left\{
\begin{array}
{lll}
\hat{r}_{j+1} & = & \hat{r}_j+\l...
...heta} \over \partial r}\right]_j \Delta r \\ \end{array}\right.\end{displaymath}](img36.gif) |
(8) |
where j is the index of the grid in the radius direction.
Finally, the calculated operators are mapped from polar coordinates to Cartesian
coordinates.





Next: APPLYING THE OPERATORS TO
Up: CALCULATING THE OPERATORS
Previous: Derivatives of surface horizontal
Stanford Exploration Project
12/18/1997
![]()
![\begin{displaymath}
\left\{
\begin{array}
{lll}
\hat{r}_{j+1} & = & \hat{r}_j+\l...
...heta} \over \partial r}\right]_j \Delta r \\ \end{array}\right.\end{displaymath}](img36.gif)