




Next: Finite difference calculation of
Up: CALCULATING THE OPERATORS
Previous: Derivatives of traveltimes
Another set of variables involved in
partial differential equation (4)
are partial derivatives of surface horizontal slownesses. According to
the definition in equation (2), we can calculate these dependent
variables by using a finite difference approximation. In Cartesian coordinates,
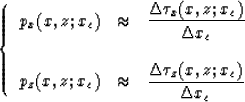
and in polar coordinates,
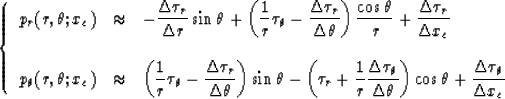
where xc=xs or xr. There are two drawbacks to using
these equations. The first is the property of the difference
operators that I have mentioned before. The second disadvantage is that
calculating the traveltime-changes with respect to the change of shot or
receiver position requires us to compute the partial derivatives of traveltimes
at least twice at the neighbor points, which significantly complicates
the algorithm.
The solution to this problem is to find the partial differential
equations for p. Appendix A shows that p satisfies the following
partial differential equation:
| 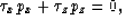 |
(5) |
which implies the orthogonal relation between rays and wavefront.
The equivalent of this equation in polar coordinates is
| 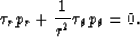 |
(6) |
To solve this equation, we can use the same algorithm as the one used for
traveltime calculation. Let us use the equation in polar coordinates as
an example. We define
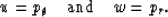
Equation (6) can then be rewriten as
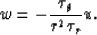
Because
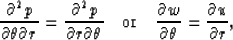
we have the transformed partial differential equation
| ![\begin{displaymath}
{\partial u \over \partial r} = - {\partial \over \partial \theta}
\left[{\tau_\theta \over r^2 \tau_r}u\right].\end{displaymath}](img31.gif) |
(7) |
If s0 is the slowness at the origin of polar coordinates, then the
initial conditions are
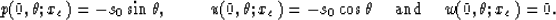
We can solve equation (7) by using the standard up-wind
finite-difference method. The direct results are the partial derivatives of
p which appear in equation (4).





Next: Finite difference calculation of
Up: CALCULATING THE OPERATORS
Previous: Derivatives of traveltimes
Stanford Exploration Project
12/18/1997
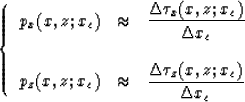
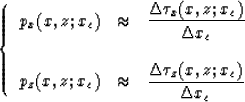
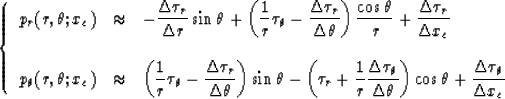
![]()
![]()
![]()
![]()