




Next: An insight into the
Up: Popovici : FD Traveltime
Previous: Introduction
The Engquist-Osher scheme used by Van Trier and Symes is an
interesting balance between computational speed and
precision. Although the scheme
introduces approximations in the calculation
of the travel time field that can be adverse for accurate
calculations of differential operators (which involve the
local derivative of the traveltime field), the scheme is more
stable than a straightforward finite-difference scheme.
In spite of all the instability problems one may
encounter using this algorithm, all of the
simpler alternatives I have tried are stable only for much smaller
grid sizes.
The fundamental algorithm described by Van Trier and Symes (1989)
is based on the eikonal equation
where
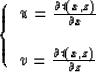
and where s(x,z) is the 2-dimensional slowness model and t(x,z) is the
travel time field.
The second equation used is the equality of the
partial derivatives of the fields u(x,z) and v(x,z),
| 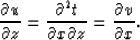 |
(2) |
In cylindrical coordinates the eikonal equation becomes
| 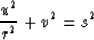 |
(3) |
where
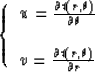
and the mixed partial derivatives are
| 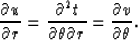 |
(4) |
The finite difference implementation of equations (1),
(2) and in cylindrical coordinates (3), (4)
is based on advancing the computational
front for the functions u(x,z) and v(x,z).
The traveltime field t(x,z) is found subsequently by integrating
the function 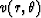 with respect to r.
In cylindrical coordinates the scheme is based on using equation (4)
to compute the values of
with respect to r.
In cylindrical coordinates the scheme is based on using equation (4)
to compute the values of 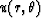 on a new computational
front of constant radius, by using the values of
on a new computational
front of constant radius, by using the values of
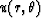 and
and 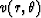 from
the previous computational front. Equation (4) becomes
from
the previous computational front. Equation (4) becomes
| 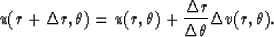 |
(5) |
Starting with a constant velocity condition in the immediate vicinity
of the source location 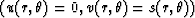 ,we can advance the computational front using the finite-difference
equation (5).
Once the values of
,we can advance the computational front using the finite-difference
equation (5).
Once the values of 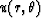 are known, the values of
are known, the values of
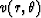 can be computed using the eikonal equation:
can be computed using the eikonal equation:
| 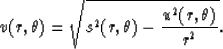 |
(6) |





Next: An insight into the
Up: Popovici : FD Traveltime
Previous: Introduction
Stanford Exploration Project
12/18/1997
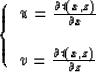
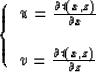
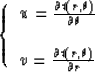
![]() with respect to r.
In cylindrical coordinates the scheme is based on using equation (4)
to compute the values of
with respect to r.
In cylindrical coordinates the scheme is based on using equation (4)
to compute the values of ![]() on a new computational
front of constant radius, by using the values of
on a new computational
front of constant radius, by using the values of
![]() and
and ![]() from
the previous computational front. Equation (4) becomes
from
the previous computational front. Equation (4) becomes