In the 2-D case equation (3) keeps the same form but
![]() is now a one-dimensional representation of the bi-dimensional
displacement field. If we use indices i and j to specify a given
cell (or a position in the plane), and indices x and z to denote the
horizontal and vertical components of
is now a one-dimensional representation of the bi-dimensional
displacement field. If we use indices i and j to specify a given
cell (or a position in the plane), and indices x and z to denote the
horizontal and vertical components of ![]() , the one-dimensional
representation of
, the one-dimensional
representation of ![]() will be a
will be a ![]() vector given by
vector given by
![]()
Appendix A shows that for a 2-D system, the operator ![]() of
equation (3) takes the form of
a
of
equation (3) takes the form of
a ![]() sparse matrix with diagonal structure.
This operator has only 13 effective terms corresponding to
17 non-vanishing diagonals as illustrated in Figure
sparse matrix with diagonal structure.
This operator has only 13 effective terms corresponding to
17 non-vanishing diagonals as illustrated in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
which was computed for an isotropic model of size 8 by 8 (64 cells).
,
which was computed for an isotropic model of size 8 by 8 (64 cells).
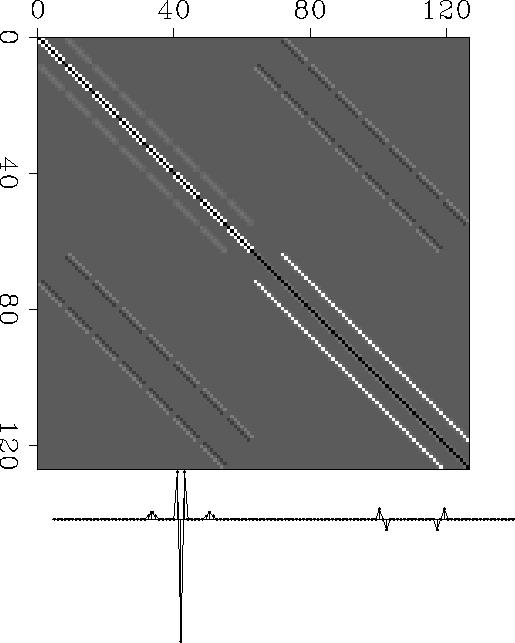 |
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the ``equivalent differencing stars" associated
with
shows the ``equivalent differencing stars" associated
with ![]() for the case of a homogeneous medium. It's worthwhile to
notice that the ux - ux star for C55 represents an x-smoothed
version of
for the case of a homogeneous medium. It's worthwhile to
notice that the ux - ux star for C55 represents an x-smoothed
version of ![]() . This form is similar to the
McClellan transform used by Hale (1990) to construct a numerically
isotropic 3-D migration operator. Here however, the suitable form of
the star comes naturally, from the direct application of physical
laws.
. This form is similar to the
McClellan transform used by Hale (1990) to construct a numerically
isotropic 3-D migration operator. Here however, the suitable form of
the star comes naturally, from the direct application of physical
laws.
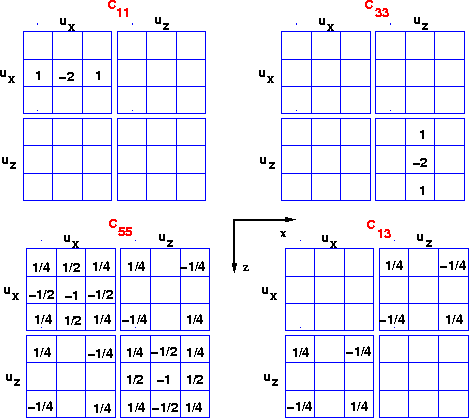 |
The method is implemented here by first reducing the operator to
tridiagonal form using an algorithm based in Givens rotations
and then using a tridiagonal eigenvalue decomposition routine.
For an n by n matrix, the cost in both stages (reduction and decomposition)
is proportional to n3, which in this case represents ![]() .
Whereas the cost in the reduction stage can be substantially reduced
with the use of a more specific algorithm that takes advantage of
the sparseness of
.
Whereas the cost in the reduction stage can be substantially reduced
with the use of a more specific algorithm that takes advantage of
the sparseness of ![]() , the price of the decomposition stage
is still extremely high.
, the price of the decomposition stage
is still extremely high.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a time frame of the horizontal component
of the displacement wavefield evaluated with the eigenvalue-decomposition
modeling for a two-layer model. The upper part (
shows a time frame of the horizontal component
of the displacement wavefield evaluated with the eigenvalue-decomposition
modeling for a two-layer model. The upper part (![]() 3/4) is isotropic,
while the bottom is transverse isotropic, with a total size of
37 by 37 cells, and a vertical impulsive displacement source at the center.
3/4) is isotropic,
while the bottom is transverse isotropic, with a total size of
37 by 37 cells, and a vertical impulsive displacement source at the center.
 |