Although the eigenvalue decomposition is unconditionally stable
and precise, the N3-dependence of the computation time makes it
prohibitively expensive. To make the method affordable,
I have derived a scheme that uses a time
propagator operator to find the solution at time ![]() ,using only the solution at time t. The basic principle is the
same used by Dablain (1986) to derive a fourth order in time, explicit,
finite difference scheme. Contrary to the method presented here,
Dablain's scheme used two time-step solutions (
,using only the solution at time t. The basic principle is the
same used by Dablain (1986) to derive a fourth order in time, explicit,
finite difference scheme. Contrary to the method presented here,
Dablain's scheme used two time-step solutions (![]() and
and ![]() ) in order to find
) in order to find ![]() .
.
A recursive solution in the time domain can be obtained with the use of the following relations:
![]()
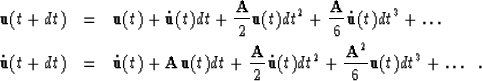 |
(7) | |
Combining these two equations, we obtain the time-propagation equation
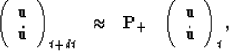
![\begin{displaymath}
{\bf P_{+}} = \left[ \begin{array}
{cc} {\bf I} + {{\bf A} \...
...\right) &
{\bf I} + {{\bf A} \over 2} dt^2 \end{array} \right]\end{displaymath}](img58.gif) |
(8) |
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows one frame of the horizontal displacement field,
for the same source and media used to generate the synthetic data of
Figure
shows one frame of the horizontal displacement field,
for the same source and media used to generate the synthetic data of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (but with a finer grid spacing, and at a different
time frame). This algorithm was implemented in the Connection Machine
C2 with parellization in both spatial axes.
(but with a finer grid spacing, and at a different
time frame). This algorithm was implemented in the Connection Machine
C2 with parellization in both spatial axes.
 |
Stability and energy conservation associated with the truncation of the Taylor expansion in equation (8) are discussed in Appendix B.