




Next: CONCLUSIONS
Up: Lumley: Prestack impedance inversion
Previous: Impedance estimation
I now briefly discuss the 2-D pilot study I have conducted to indicate
the practical utility of my prestack impedance inversion theory
and algorithms.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows two CMP gathers from a 1970's vintage 2-D marine survey. The gathers
are from midpoint location 1 km and 2 km respectively, along the stacked
section shown in Figure
shows two CMP gathers from a 1970's vintage 2-D marine survey. The gathers
are from midpoint location 1 km and 2 km respectively, along the stacked
section shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The CMP gathers exhibit a strong
amplitude-offset (AVO) reflectivity response on the reflected event at
about 2.3 seconds zero-offset time. Note the offset-variability in the raw AVO
response. An advantage of prestack migration/inversion is that it uses
an estimated variable velocity field to compensate for such wave-based
focusing/defocusing effects on amplitudes in raw data.
. The CMP gathers exhibit a strong
amplitude-offset (AVO) reflectivity response on the reflected event at
about 2.3 seconds zero-offset time. Note the offset-variability in the raw AVO
response. An advantage of prestack migration/inversion is that it uses
an estimated variable velocity field to compensate for such wave-based
focusing/defocusing effects on amplitudes in raw data.
The stacked section shows a few strong reflectors in the
2.3-2.5 second range, which are known to correspond to the reservoir interval
of a producing gas field (Kjartansson, 1979). The offset stack across any AVO
character will tend to invalidate the common assumption that the stacked
section is an approximation of P impedance contrasts. This would
have a negative impact on ``poststack impedance inversion'' for example.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the migration velocity semblance panels corresponding
to the two CMP positions. The overlain black curves are the ``optimal''
migration velocities picked by a nonlinear Monte Carlo automatic
search algorithm (Lumley, 1992b).
After all 100 semblance scans are searched for the optimal
migration velocity trajectory, the results are slightly smoothed and contoured
in Figure
shows the migration velocity semblance panels corresponding
to the two CMP positions. The overlain black curves are the ``optimal''
migration velocities picked by a nonlinear Monte Carlo automatic
search algorithm (Lumley, 1992b).
After all 100 semblance scans are searched for the optimal
migration velocity trajectory, the results are slightly smoothed and contoured
in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The contours of the migration velocity field range
from 1.6 km/s at the top to 2.3 km/s at the bottom, in 0.1 km/s intervals.
The low velocity zone at the far left is apparently real, when the
semblance scans at this location are examined. Also, note the low rms
velocity zone at 2.3 seconds in the right scan, which will later be shown
to correlate with an impedance anomaly indicative of increased gas saturation.
This velocity model is used for the subsequent reflectivity estimation and
impedance inversion.
. The contours of the migration velocity field range
from 1.6 km/s at the top to 2.3 km/s at the bottom, in 0.1 km/s intervals.
The low velocity zone at the far left is apparently real, when the
semblance scans at this location are examined. Also, note the low rms
velocity zone at 2.3 seconds in the right scan, which will later be shown
to correlate with an impedance anomaly indicative of increased gas saturation.
This velocity model is used for the subsequent reflectivity estimation and
impedance inversion.
Given 4800 input seismic traces, I perform 48 constant offset migrations
ranging from offsets of 0.25 km to 2.65 km in 50 m increments. Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows two Common Reflection Point (CRP) slices of the
constant offset migration cube, each
slice taken at a fixed midpoint position of 1 km and 2 km respectively, to
correspond with the surface positions of the previous figures.
This figure corresponds to the prestack-migrated equivalent of an
NMO/DMO amplitude-corrected CMP gather in conventional AVO processing.
The midpoint
coordinate direction is perpendicular to the plane of the page. The top
of the reservoir is at 2.3 seconds, and we are looking at how the
migrated reflectivity estimate varies as a function of offset:
shows two Common Reflection Point (CRP) slices of the
constant offset migration cube, each
slice taken at a fixed midpoint position of 1 km and 2 km respectively, to
correspond with the surface positions of the previous figures.
This figure corresponds to the prestack-migrated equivalent of an
NMO/DMO amplitude-corrected CMP gather in conventional AVO processing.
The midpoint
coordinate direction is perpendicular to the plane of the page. The top
of the reservoir is at 2.3 seconds, and we are looking at how the
migrated reflectivity estimate varies as a function of offset: 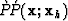 .At surface position 1 km, the top panel shows what appears to be a weak
negative polarity reflection at the top of the reservoir, and the reflection
strength approximately constant, although somewhat irregular,
with increasing offset (angle). At the 2 km surface
position (lower panel), the top of the reservoir appears to have changed to a
somewhat stronger negative polarity and an increase in negative amplitude
with increasing offset (angle). This
difference suggests that the material properties in the reservoir have
changed spatially from surface position 1 km to 2 km.
.At surface position 1 km, the top panel shows what appears to be a weak
negative polarity reflection at the top of the reservoir, and the reflection
strength approximately constant, although somewhat irregular,
with increasing offset (angle). At the 2 km surface
position (lower panel), the top of the reservoir appears to have changed to a
somewhat stronger negative polarity and an increase in negative amplitude
with increasing offset (angle). This
difference suggests that the material properties in the reservoir have
changed spatially from surface position 1 km to 2 km.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is the same plot as Figure
is the same plot as Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , except the
quantity being plotted is the incident reflection angle
, except the
quantity being plotted is the incident reflection angle 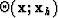 instead of the reflectivity itself. The contours range from reflection
angles of
instead of the reflectivity itself. The contours range from reflection
angles of 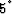 at near offsets to
at near offsets to 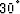 at the farthest offsets, in
increments of
at the farthest offsets, in
increments of 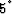 . Given the functions
. Given the functions 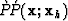 and
and
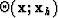 estimated from the data, the two can be combined to
give the estimate of reflectivity as a function of reflection angle:
estimated from the data, the two can be combined to
give the estimate of reflectivity as a function of reflection angle:
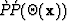 .
.
For comparative purposes, I plot the prestack migrated stack in Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . This is obtained efficiently by merely summing the
. This is obtained efficiently by merely summing the
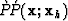 gathers over the offset coordinate
gathers over the offset coordinate 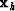 . It will be
interesting to compare this image with the P and S impedance contrast
maps.
. It will be
interesting to compare this image with the P and S impedance contrast
maps.
Next,
at each point in earth, I perform the linearized inversion of 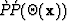 to estimate the elastic parameters
to estimate the elastic parameters 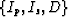 . The P impedance contrast
section is shown in Figure
. The P impedance contrast
section is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , the S impedance contrast
section is shown in Figure
, the S impedance contrast
section is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , and the density contrast section
is shown in Figure
, and the density contrast section
is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . As expected, the S/N ratio and stability
of the inversion is good for P impedance, medium for S impedance, and
very poor for density. Figure
. As expected, the S/N ratio and stability
of the inversion is good for P impedance, medium for S impedance, and
very poor for density. Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) justifies my claim that there
is little or no useful independent information about subsurface
density contrasts in standard acquisition geometry surface seismic data.
Disregarding density, there appear to be some
significant differences in information content comparing the P and S
impedance contrast sections, especially near the 2 km midpoint location.
Also, the migration stack of Figure
justifies my claim that there
is little or no useful independent information about subsurface
density contrasts in standard acquisition geometry surface seismic data.
Disregarding density, there appear to be some
significant differences in information content comparing the P and S
impedance contrast sections, especially near the 2 km midpoint location.
Also, the migration stack of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is most similar to the
P impedance contrast section of Figure
is most similar to the
P impedance contrast section of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , as expected, but
does have some orthogonal information content along the reservoir reflector
at 2.3 seconds in the distance range of 1.2-1.6 km, for example.
, as expected, but
does have some orthogonal information content along the reservoir reflector
at 2.3 seconds in the distance range of 1.2-1.6 km, for example.
A simple multiplication of the P and S sections produces
an interesting P*S anomaly map,
as shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . In ``normal'' rock sequences, the P and
S impedance contrasts are usually of the same polarity, and hence plot
dark gray to black (blue) in Figure
. In ``normal'' rock sequences, the P and
S impedance contrasts are usually of the same polarity, and hence plot
dark gray to black (blue) in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
However, in a transition zone
of changing rock properties, say from brine to gas-filled porespace, the
P and S impedance contrasts may be of opposite polarity, and will plot as
white (red) regions in Figure
.
However, in a transition zone
of changing rock properties, say from brine to gas-filled porespace, the
P and S impedance contrasts may be of opposite polarity, and will plot as
white (red) regions in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . It is interesting to note that the
white (red) anomalous regions of Figure
. It is interesting to note that the
white (red) anomalous regions of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) are well localized to the
reflectors associated with the producing gas reservoir interval, and
also importantly, nowhere else in the section.
are well localized to the
reflectors associated with the producing gas reservoir interval, and
also importantly, nowhere else in the section.
This result indicates that the prestack impedance inversion theory and
algorithms have been qualitatively tested and give reasonable physical
results, since an AVO amplitude anomaly and a P*S impedance
anomaly has been unambiguously detected by the method at the zone of a
known gas producing reservoir interval.





Next: CONCLUSIONS
Up: Lumley: Prestack impedance inversion
Previous: Impedance estimation
Stanford Exploration Project
11/17/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows two CMP gathers from a 1970's vintage 2-D marine survey. The gathers
are from midpoint location 1 km and 2 km respectively, along the stacked
section shown in Figure
shows two CMP gathers from a 1970's vintage 2-D marine survey. The gathers
are from midpoint location 1 km and 2 km respectively, along the stacked
section shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The CMP gathers exhibit a strong
amplitude-offset (AVO) reflectivity response on the reflected event at
about 2.3 seconds zero-offset time. Note the offset-variability in the raw AVO
response. An advantage of prestack migration/inversion is that it uses
an estimated variable velocity field to compensate for such wave-based
focusing/defocusing effects on amplitudes in raw data.
. The CMP gathers exhibit a strong
amplitude-offset (AVO) reflectivity response on the reflected event at
about 2.3 seconds zero-offset time. Note the offset-variability in the raw AVO
response. An advantage of prestack migration/inversion is that it uses
an estimated variable velocity field to compensate for such wave-based
focusing/defocusing effects on amplitudes in raw data.