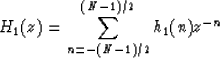
The usual method in designing 2-D filters is to design an optimum filter that corresponds to a given desired two-dimensional spectrum. For designing 2-D filters that exhibit some special symmetry properties usually some transformation techniques are used to exploit the symmetry. The most common method used for generating a 2-D circularly symmetric filter is to use a transformation filter to generate the equivalent 2-D filter given the corresponding filter along one direction. This is done using a transformation filter called the McClellan transformation represented by F(k). The method requires one one-dimensional spectral expansion to get the filter coefficients for the 1-D problem and one two-dimensional spectral expansion to generate the transformation filter.
The particular method for realizing these filters that yields structures with low sensitivity and low computational complexity is one proposed by McClellan and Chan 1977. The steps involved in this method are as follows.
A 1-D nonrecursive filter of odd length can be represented by the transfer function
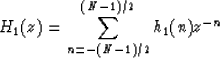 |
(1) |
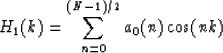 |
(2) |
![]()
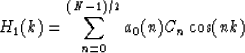
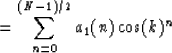 |
(3) |
| cos(k) = A cos(kx) + B cos(ky) + C cos(kx) cos(ky) + D | (4) |
= F(kx,ky)
where A,B,C, and D are constants. In the original McClellan transformation A=B=C=0.5 and D=-0.5. The McClellan filter is an approximation to the circular filter![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The modified filter has better accuracy at
higher wavenumbers as can be seen from the contours.
Applying the McClellan transformation
to the frequency response of a 1-D nonrecursive filter given in Equation
3 yields
.
The modified filter has better accuracy at
higher wavenumbers as can be seen from the contours.
Applying the McClellan transformation
to the frequency response of a 1-D nonrecursive filter given in Equation
3 yields
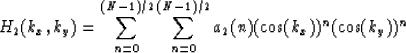 |
(5) |
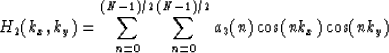 |
(6) |
This frequency response can be realized using the chebyshev filter
structure shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . The upper part of the structure
does the Chebyshev recursion and the lower part implements the
convolution with the one-dimensional filter.
. The upper part of the structure
does the Chebyshev recursion and the lower part implements the
convolution with the one-dimensional filter.
|
mco3
Figure 1 Contours of constant amplitude and phase for the original McClellan transformation filter(large dash), the modified McClellan transformation filter (dot dash) and the ideal circularly symmetric filter (continuous). |  |
 |