




Next: Remapping in
Up: Introduction
Previous: Introduction
The constant velocity prestack migration
in offset-midpoint coordinates can be formulated as:
| 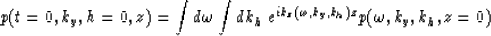 |
(1) |
where 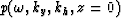 is the 3-D Fourier transform
of the field p(t,y,h,z=0) recorded at the surface, using
Claerbout's (1985) sign convention:
is the 3-D Fourier transform
of the field p(t,y,h,z=0) recorded at the surface, using
Claerbout's (1985) sign convention:
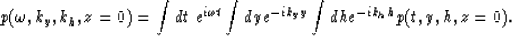
The constant 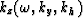 is defined in the
dispersion relation as
is defined in the
dispersion relation as
| ![\begin{displaymath}
{k_z(\omega,k_y,k_h)} \equiv
{ -{\omega \over v} \left\{ \le...
...2 \over {4\omega^2}}
(k_y-k_h)^2\right]^{1 \over 2} \right\} }.\end{displaymath}](img6.gif) |
(2) |
The constant velocity zero-offset migration
in offset-midpoint coordinates can be formulated as:
| 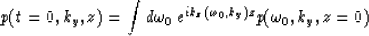 |
(3) |
where 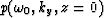 is the 2-D Fourier transform
of the field p(t,y,z=0).
The constant
is the 2-D Fourier transform
of the field p(t,y,z=0).
The constant 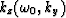 is defined in the
dispersion relation as
is defined in the
dispersion relation as
| ![\begin{displaymath}
{k_z(\omega_0,k_y)} \equiv
{ -{{2 \omega_0} \over v} {\left[
1-{{v^2 k_y^2} \over {4 \omega_0^2}}\right]}^{1 \over 2}}.\end{displaymath}](img10.gif) |
(4) |
The goal of the ensuing derivation is to convert
equation (1) into a form similar to equation (3).
Using a change of variables and integrating over the
variable kh, equation (1) will be transformed
into the form:
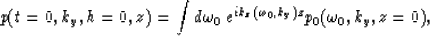
where 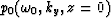 represents the zero-offset data field.
Following Hale's (1983) derivation,
a new variable
represents the zero-offset data field.
Following Hale's (1983) derivation,
a new variable 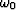 is introduced in order to
isolate the zero-offset migration operator.
The variable
is introduced in order to
isolate the zero-offset migration operator.
The variable 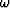 is expressed as
is expressed as
| ![\begin{displaymath}
\omega \equiv
{\omega_0 { \left[ 1+{ {v^2 k_h^2 } \over
{ 4 \omega_0^2-v^2 k_y^2}} \right]}^{1 \over 2}},\end{displaymath}](img15.gif) |
(5) |
where 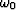 is considered variable and ky, kh are
constant.
Substituting
is considered variable and ky, kh are
constant.
Substituting 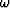 in equation (2),
the downward continuation operator
in equation (2),
the downward continuation operator 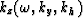 is transformed into
is transformed into
| ![\begin{displaymath}
k_z \equiv
-{ {2 \omega_0} \over v} {\left[ 1 -
{{v^2 k_y^2} \over {4 \omega_0^2}} \right]}^{1 \over 2}\end{displaymath}](img16.gif) |
(6) |
which now has the same form as the operator in
equation (4).
In order to isolate the zero-offset
migration operator, the variable
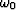 is substituted for
is substituted for 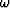 in equation (1)
and the order
of integration is changed between
in equation (1)
and the order
of integration is changed between 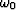 and kh.
The integration
boundaries have to be observed carefully
as they are modified after each change of variables
and integration order. However, for the sake of simplicity, I will
ignore in the following demonstration the integration
limits, which are discussed in Appendix A.
and kh.
The integration
boundaries have to be observed carefully
as they are modified after each change of variables
and integration order. However, for the sake of simplicity, I will
ignore in the following demonstration the integration
limits, which are discussed in Appendix A.
For simplicity I define the variables
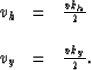
By substituting the variable
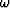 with the expression in
with the expression in 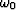 in equation (1)
and changing the integration order between
in equation (1)
and changing the integration order between 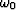 and kh
the prestack migration equation becomes
and kh
the prestack migration equation becomes
| 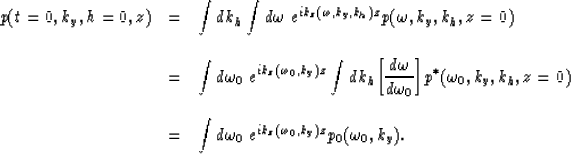 |
(7) |
The new field 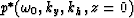 represents a remapping
(interpolation) from
represents a remapping
(interpolation) from 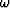 to
to 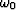 of the field
of the field 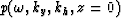 .The meaning of this remapping will be discussed
in the next section.
The field
.The meaning of this remapping will be discussed
in the next section.
The field 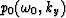 defined as
defined as
| ![\begin{displaymath}
p(\omega_0,k_y)=\int dk_h
{\left[{{d \omega} \over {d \omega_0}}\right]}
p^*(\omega_0,k_y,k_h,z=0)\end{displaymath}](img21.gif) |
(8) |
with the Jacobian
| ![\begin{displaymath}
\begin{array}
{lcl}
J & = & \displaystyle{
{\left[{{d \omega...
..._h^2 v_y^2} \over
{ (\omega_0^2-v_y^2)^2}} \right ]}\end{array}\end{displaymath}](img22.gif) |
(9) |
represents the zero-offset field.
The last equation in (7) represents zero-offset downward
continuation and imaging as introduced by Gazdag (1978)
or Stolt (1978). Equation (8) represents a
way of obtaining the zero-offset section from constant-offset
sections.
So far the operations needed to obtain the zero-offset
stacked section from the constant-offset field are:
- 1.
- Fourier transform the constant-offset field
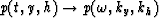 .
. - 2.
- Remap (interpolate) the
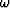 axis into
axis into 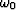 .
. - 3.
- Multiply by the Jacobian.
- 4.
- Integrate over kh.
- 5.
- Inverse Fourier transform
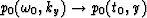 .
.





Next: Remapping in
Up: Introduction
Previous: Introduction
Stanford Exploration Project
11/17/1997
![]()
![\begin{displaymath}
{k_z(\omega,k_y,k_h)} \equiv
{ -{\omega \over v} \left\{ \le...
...2 \over {4\omega^2}}
(k_y-k_h)^2\right]^{1 \over 2} \right\} }.\end{displaymath}](img6.gif)
![\begin{displaymath}
{k_z(\omega_0,k_y)} \equiv
{ -{{2 \omega_0} \over v} {\left[
1-{{v^2 k_y^2} \over {4 \omega_0^2}}\right]}^{1 \over 2}}.\end{displaymath}](img10.gif)
![]()
![\begin{displaymath}
\omega \equiv
{\omega_0 { \left[ 1+{ {v^2 k_h^2 } \over
{ 4 \omega_0^2-v^2 k_y^2}} \right]}^{1 \over 2}},\end{displaymath}](img15.gif)
![\begin{displaymath}
k_z \equiv
-{ {2 \omega_0} \over v} {\left[ 1 -
{{v^2 k_y^2} \over {4 \omega_0^2}} \right]}^{1 \over 2}\end{displaymath}](img16.gif)
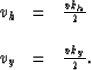
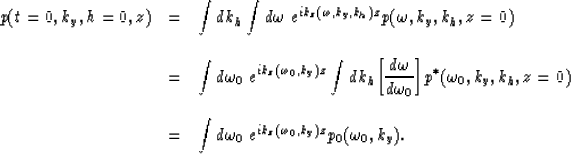
![\begin{displaymath}
\begin{array}
{lcl}
J & = & \displaystyle{
{\left[{{d \omega...
..._h^2 v_y^2} \over
{ (\omega_0^2-v_y^2)^2}} \right ]}\end{array}\end{displaymath}](img22.gif)