




Next: PDE
Up: Introduction
Previous: MZO from prestack migration
As the variable
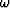 is replaced with
is replaced with 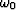 in the integral
in the integral
![\begin{displaymath}
\int d\omega p(\omega,k_y,k_h)=
\int d\omega_0 {\left[{{d \omega} \over {d \omega_0}}\right]}
p^*(\omega_0,k_y,k_h),\end{displaymath}](img25.gif)
each value of 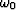 in the integral
needs to be associated with the appropriate value of the field
in the integral
needs to be associated with the appropriate value of the field
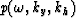 which is
which is
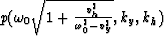 .The new field
.The new field 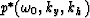 represents
a remapping of the original field
represents
a remapping of the original field 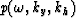 .Each value in the new field
.Each value in the new field 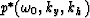 with
coordinates
with
coordinates 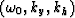 corresponds to the value
in the field
corresponds to the value
in the field 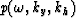 with coordinates
with coordinates
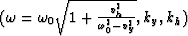 .
.
The 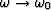 remapping can be understood easier
if one takes the particular case ky=0.
The change of variable in
remapping can be understood easier
if one takes the particular case ky=0.
The change of variable in 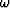 (5) becomes
(5) becomes
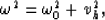
the Jacobian
![\begin{displaymath}
{\left[ {{d \omega} \over {d \omega_0}} \right]}=
{{\mid {{2...
...over v} \mid} \over
{\sqrt{{{4\omega_0^2} \over v^2}+k_h^2}}},\end{displaymath}](img33.gif)
and the zero-offset migrated field becomes
| 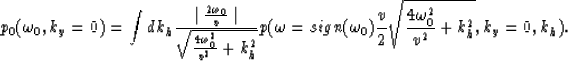 |
(10) |
Compare equation (10) with the Gazdag (1978) and
Stolt (1978) zero-offset migration equations:
| 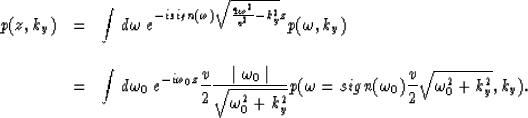 |
(11) |
Notice that the Stolt migration formula is comprised of an
inverse Fourier transform and a remapping (interpolation).
Equation (10) inside the integral in kh
has the same form
as the remapping in the Stolt formula, save for a constant
coefficient  . This similitude suggests the equivalent
formulation:
. This similitude suggests the equivalent
formulation:
| 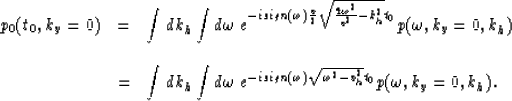 |
(12) |
The validity of the new equation is verified
by replacing in equation (12) the
exponential expression
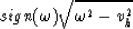
by a new variable 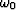 to get back the inverse Fourier transform
of the initial expression.
to get back the inverse Fourier transform
of the initial expression.
The integration in kh represents the inverse Fourier
transform at zero offset (h=0). However because
equation (12) actually performs summation along
hyperbolas in the spatial coordinate h, replacing
the integral in kh by the inverse Fourier transform will not
return the constant-offset sections.
Applying the same technique to the case 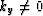 I obtain
I obtain
| ![\begin{displaymath}
p_0(t_0,k_y)=
\int dk_h \int d\omega \;
e^{-isign(\omega)
{\...
...h^2)^2-4\omega^2v_y^2})\right]}^{1\over2}t_0}
p(\omega,k_y,k_h)\end{displaymath}](img40.gif) |
(13) |
which can be verified by substituting the exponential
expression in 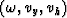 with a new variable
with a new variable 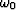 defined as
defined as
| ![\begin{displaymath}
\omega_0^2 = {1 \over 2}
\left [ {\omega^2+v_y^2-v_h^2 +
{\sqrt {(\omega^2+v_y^2-v_h^2)^2-4 \omega^2 v_y^2}}} \right ].\end{displaymath}](img42.gif) |
(14) |





Next: PDE
Up: Introduction
Previous: MZO from prestack migration
Stanford Exploration Project
11/17/1997
![]() is replaced with
is replaced with ![]() in the integral
in the integral
![]()
![]() remapping can be understood easier
if one takes the particular case ky=0.
The change of variable in
remapping can be understood easier
if one takes the particular case ky=0.
The change of variable in ![]() (5) becomes
(5) becomes
![]()
![\begin{displaymath}
{\left[ {{d \omega} \over {d \omega_0}} \right]}=
{{\mid {{2...
...over v} \mid} \over
{\sqrt{{{4\omega_0^2} \over v^2}+k_h^2}}},\end{displaymath}](img33.gif)
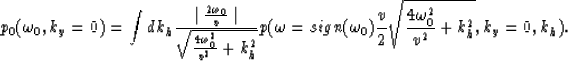
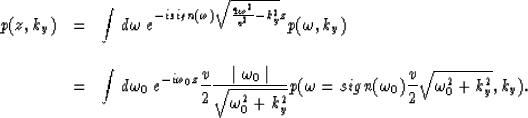
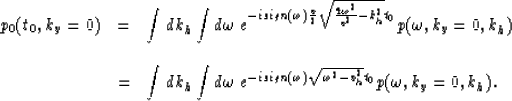
![]()
![]() I obtain
I obtain