Generalized scattering

To proceed, we use isotropic elastic WKBJ (ray-valid) Green's tensors for P waves of the form:

 

$${\bf u}^{^{P}}({\bf x};{\bf x}^{^{\prime}}) = A^{^{P}}({\bf ... ...^{\prime}})} = A^{^{P}}{\bf \hat{t}}^{^{P}}e^{i\omega\tau} \;,$$ (16)

where A^<<860>>P and $\tau$ are the ray-valid P-wave amplitude and traveltime from the ``source'' location ${\bf x}^{^{\prime}}$ to the ``observation'' point ${\bf x}$.The unit vector ${\bf \hat{t}}^{^{P}}$ is the direction parallel to P-wave propagation, and is perpendicular to the wavefronts $\tau = \mbox{constant}$.Given the definition of ${\bf u}^{^{P}}$ in (16), we derive the following useful quantities:

 

$$\vert {\bf u}^{^{P}}\vert = {\bf u}^{^{P}}{\bf \cdot}{\bf \hat{t}}^{^{P}}= A^{^{P}}e^{i\omega\tau} \;,$$ (17)

 

$$\nabla{\bf \cdot}{\bf u}^{^{P}}= i\omega\nabla\tau{\bf \cdot... ...omega\tau} = \frac{i\omega}{\alpha}\vert{\bf u}^{^{P}}\vert \;,$$ (18)

and

 

$$\nabla{\bf u}^{^{P}}= i\omega\nabla\tau{\bf u}^{^{P}}+ \mbox... ...ox \frac{i\omega}{\alpha}{\bf \hat{t}}^{^{P}}{\bf u}^{^{P}}\;,$$ (19)

where $\alpha({\bf x})$ is the compressional wave velocity. In the gradient equation (19) for $\nabla{\bf u}^{^{P}}$ we have used the fact that

 

$$\nabla\tau = \frac{1}{\alpha} {\bf \hat{t}}^{^{P}}\;,$$ (20)

which follows from the ray eikonal equation defining the traveltime $\tau$:

 

$$\vert \nabla\tau \vert^2 = \nabla\tau{\bf \cdot}\nabla\tau = \frac{1}{\alpha^2} \;,$$ (21)

(Cervený et al., 1977), and the farfield approximation that

$$\frac{\vert\nabla A^{^{P}}\vert}{\vert A^{^{P}}\vert} \ll 1 \;,$$ (22)

since $A\sim 1/r$ and so $\vert\nabla A\vert \sim 1/r^2$.

Now, we choose $\u_1 \equiv {\bf u}^{^{P}}({\bf x};{\bf x}_s)$ to get the P-wave reflectivity response at the subsurface point ${\bf x}$ from the source location ${\bf x}_s$.Under the previous assumption of linear elastic isotropy for ${\bf u}^{^{P}}$, the stress-strain relationship is isotropic such that

 

$${\mbox{$\boldmath\sigma$}^{^{P}}}= \left[ \lambda(\nabla{\bf... ...{P}}){\bf I}+ 2\mu{\bf \hat{t}}^{^{P}}{\bf u}^{^{P}}\right] \;,$$ (23)

where $\lambda({\bf x})$ and $\mu({\bf x})$ are the Lamé parameters, and ${\bf I}$ is the second-order identity matrix $\delta_{ij}$.The expression for the divergence of the stress field becomes

 

$$\nabla{\bf \cdot}{\mbox{$\boldmath\sigma$}^{^{P}}}= \mbox{term 1} + \mbox{term 2} \;,$$ (24)

where

 

$$\mbox{term 1} = \frac{i\omega}{\alpha}\left[ \lambda\nabla({... ...abla{\bf \cdot}({\bf \hat{t}}^{^{P}}{\bf u}^{^{P}}) \right] \;,$$ (25)

and

 

$$\mbox{term 2} = \frac{i\omega}{\alpha^2}\left[ (\alpha\nabla... ...pha){\bf \cdot}({\bf \hat{t}}^{^{P}}{\bf u}^{^{P}}) \right] \;,$$ (26)

where we have used the identities:

 

$$\nabla{\bf \cdot}(\alpha{\bf I}) = \nabla\alpha\;,$$ (27)

and

 

$$\nabla{\bf \cdot}(\alpha{\mbox{$\boldmath\sigma$}}) = \alpha... ...\sigma$}}+ \nabla\alpha{\bf \cdot}{\mbox{$\boldmath\sigma$}}\;,$$ (28)

for any scalar $\alpha$ and second order tensor ${\mbox{$\boldmath\sigma$}}$ (Ben-Menahem and Singh, 1981, p.953). Now, using the identity

 

$$\nabla{\bf \cdot}(\u{\bf v}) = (\nabla{\bf \cdot}\u){\bf v}+ \u{\bf \cdot}\nabla{\bf v}\;,$$ (29)

for any two vectors $\u$ and ${\bf v}$, and the fact that

 

$$\nabla{\bf \cdot}{\bf \hat{t}}^{^{P}}= 0 \;,$$ (30)

we rewrite (25) as

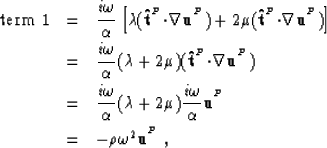$$\begin{eqnarray} \mbox{term 1} & = & \frac{i\omega}{\alpha}\left[ \lambda({\bf \... ...a}{\bf u}^{^{P}}\nonumber \\ & = & -\rho\omega^2{\bf u}^{^{P}}\;,\end{eqnarray}$$ (31)

where we have used (18) and the definition:

 

$$\lambda+ 2\mu = \rho\alpha^2 \;.$$ (32)

Furthermore, we compress the dot products in (26) to yield:

 

$$\mbox{term 2} = \frac{i\omega}{\alpha^2}\vert{\bf u}^{^{P}}\... ...bf \cdot}({\bf \hat{t}}^{^{P}}{\bf \hat{t}}^{^{P}}) \right] \;,$$ (33)

Recalling the elastic wave equation

 

$${\bf f}^{^{P}}= -\rho\omega^2{\bf u}^{^{P}}- \nabla{\bf \cdot}{\mbox{$\boldmath\sigma$}^{^{P}}}$$ (34)

and substituting (31) and (33) for the stress divergence term, we arrive at the following expression for the body force ${\bf f}^{^{P}}$:

 

$${\bf f}^{^{P}}= -\frac{i\omega}{\alpha^2}\vert{\bf u}^{^{P}}... ...bf \cdot}({\bf \hat{t}}^{^{P}}{\bf \hat{t}}^{^{P}}) \right] \;.$$ (35)

Equation (35) is a body force equivalent for surface reflectivity excitations, and is clearly dependent on material property contrasts (gradients): $\nabla\alpha$, $\nabla\lambda$ and $\nabla\mu$.

At this point, it is convenient to make an analogy to Born elastic scattering (Beydoun and Mendes, 1989) in that we can write

 

$$\nabla{\bf \cdot}{\mbox{$\boldmath\sigma$}^{^{P}}}= \nabla_o... ...\nabla{\bf \cdot}{\mbox{$\boldmath\sigma$}}^{^{\delta m}} \;,$$ (36)

where $\nabla_o$ is the gradient with respect to a reflectionless smooth background model, and $\nabla{\bf \cdot}{\mbox{$\boldmath\sigma$}}^{^{\delta m}}$ is the stress divergence field associated with the true model material property contrasts: $\nabla\alpha$, $\nabla\lambda$ and $\nabla\mu$, which give rise to the scattered wavefield. The two stress divergence terms can be associated with (31) and (33) such that:

 

$$\mbox{term 1} = \nabla_o{\bf \cdot}{\mbox{$\boldmath\sigma$}^{^{P}}}= -\rho\omega^2{\bf u}^{^{P}}\;,$$ (37)

which is the background wavefield, and

 

$$\mbox{term 2} = \nabla{\bf \cdot}{\mbox{$\boldmath\sigma$}}^... ... \cdot}({\bf \hat{t}}^{^{P}}{\bf \hat{t}}^{^{P}}) \right] \;,$$ (38)

which is the scattered wavefield.

To obtain the reflected field at the receiver position ${\bf x}_r$, recall the volume integral representation (15) for P waves:

 

$${\bf \hat{a}}_r{\bf \cdot}{\bf u}^{^{P}}({\bf x}_r,{\bf x}_s... ...}_s){\bf \cdot}\u_2({\bf x};{\bf x}_r)\, d{\cal V}({\bf x}) \;.$$ (39)

We substitute the WKBJ Green's tensor for the wavefield ${\bf u}^{^{P}}$ and $\u_2$ as defined by (16) and (14):

 

$${\bf u}^{^{P}}({\bf x};{\bf x}_s) = A^{^{P}}({\bf x};{\bf x}... ...) \rightarrow A_s e^{i\omega\tau_s} {\bf \hat{t}}^{^{P}}_s \;,$$ (40)

and

 

$$\u_2({\bf x};{\bf x}_r) = A^{^{P}}({\bf x};{\bf x}_r) e^{i\o... ...] \rightarrow A_r e^{i\omega\tau_r} {\bf \hat{t}}^{^{P}}_r \;,$$ (41)

where

 

$$A_r = A^{^{P}}({\bf x};{\bf x}_r) \cos {\bf \hat{a}}_r({\bf x}_r) \;,$$ (42)

and  

$$\cos a_r({\bf x}_r) = [{\bf \hat{a}}_r({\bf x}_r){\bf \cdot}{\bf \hat{t}}^{^{P}}({\bf x}_r)] \;.$$ (43)

The latter is evaluated at ${\bf x}_r$, and all other compact quantities are evaluated at ${\bf x}$.The factor $\cos a_r$ is required for multi-component displacement data. For example, if 3-component data are available, or if pressure data are recorded (marine), then $\cos a_r = 1$ and ${\bf \hat{a}}_r{\bf \cdot}{\bf u}^{^{P}}= \vert{\bf u}^{^{P}}\vert$. Or, if only vertical component data are available, then $\cos a_r$ is just the cosine of the incident arrival ray direction with respect to the normal to the recording surface at ${\bf x}_r$, and ${\bf \hat{a}}_r{\bf \cdot}{\bf u}^{^{P}}$ is the recorded vertical component u_z^<<208>>P. Substituting (35), (16) and (41) into (39) we obtain:

 

$${\bf \hat{a}}_r{\bf \cdot}{\bf u}^{^{P}}({\bf x}_r) = -\int_... ..._s) {\bf \cdot}{\bf \hat{t}}^{^{P}}_r \right\} \, d{\cal V}\;,$$ (44)

where we have compacted the notation: $\tau_{sr}=\tau_s+\tau_r$.Equation (44) defines how to forward model non-Zoeppritz, non-geometric P-P reflections and diffractions created by gradients in the material properties $\alpha$, $\lambda$ and $\mu$. We note that the concept of a single ``reflecting surface'' is generalized to three such surfaces, each defined by $\nabla\alpha$, $\nabla\lambda$ and $\nabla\mu$, which are not necessarily identical! We also note that the scattering contribution from the parameter gradients involves no plane-wave assumption, and therefore is more general than the Zoeppritz coefficients. Finally, since ${\bf \hat{t}}^{^{P}}_s$ and ${\bf \hat{t}}^{^{P}}_r$ are arbitrary incident and emergent directions at the reflecting ``surface'', they do not satisfy Snell's Law in general, and therefore create a total scattered response which is a hybrid combination of geometric plane-wave reflection (Aki and Richards, 1980), and Rayleigh-Sommerfeld diffraction (Goodman, 1968).