In this section, we now seek to distinguish the geometric (specular) reflection
contributions from the diffraction contributions to the total scattered
response derived in (44). Without loss of generality, we define
a local geometric/specular/Snell reflection wavefield ![]() such that
such that
| |
(45) |
The term ![]() is a geometric reflection coefficient, which may or may not be
related to the Zoeppritz plane-wave coefficient, as discussed later.
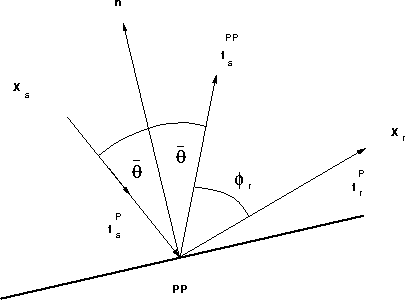
The unit vector
is a geometric reflection coefficient, which may or may not be
related to the Zoeppritz plane-wave coefficient, as discussed later.
The unit vector ![]() is the direction of geometric reflection given
by satisfying Snell's Law at the reflecting surface, as sketched in
Figure
is the direction of geometric reflection given
by satisfying Snell's Law at the reflecting surface, as sketched in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) :
:
| |
(46) |
where ![]() is the unit normal to the reflecting surface at
is the unit normal to the reflecting surface at ![]() .Given this definition of
.Given this definition of ![]() , the following identity also relates
, the following identity also relates ![]() to
to
![]() :
:
| |
(47) |
 |
We derive the following useful properties for ![]() :
:
| |
(48) |
and
| |
(49) |
Then, we evaluate the stress field ![]() associated with this geometric
reflectivity as:
associated with this geometric
reflectivity as:
| |
(50) |
Next, we decompose the total stress gradient into background and scattered stress field gradient components, as suggested by the Born analogy and physical interpretation of (36), (37) and (38):
| |
(51) |
where ![]() is the gradient with respect to a smooth (reflectionless)
background model,
is the gradient with respect to a smooth (reflectionless)
background model, ![]() refers to the direct stress
divergence wavefield in the smooth background medium, and
refers to the direct stress
divergence wavefield in the smooth background medium, and ![]() refers to the scattered (reflected) stress divergence wavefield in the
smooth background model.
There is an implicit and as yet unexplored relationship between the
Born model (36) and our Kirchhoff model (51):
refers to the scattered (reflected) stress divergence wavefield in the
smooth background model.
There is an implicit and as yet unexplored relationship between the
Born model (36) and our Kirchhoff model (51):
| |
(52) |
Our Kirchhoff decomposition (51) assumes a linear relationship between the total stress divergence in the true medium versus the direct and scattered stress divergences in the smooth background medium.
We evaluate the scattered stress divergence ![]() as:
as:
| |
(53) |
The terms of order ![]() vanish because the
gradient
vanish because the
gradient
![]() is taken with respect to the smooth reflectionless background medium,
and contains no source of scattering.
Continuing to evaluate
is taken with respect to the smooth reflectionless background medium,
and contains no source of scattering.
Continuing to evaluate ![]() :
:
 |
||
| (54) |
where we have assumed that
| |
(55) |
which implies that that propagation directions ![]() , traveltimes
, traveltimes ![]() and spreading amplitudes
and spreading amplitudes ![]() of the scattered wavefield as it propagates
from the scattering point to the observation point, are approximately
the same in the smooth background as in the true background medium.
The divergence of the total stress field in the true medium is then:
of the scattered wavefield as it propagates
from the scattering point to the observation point, are approximately
the same in the smooth background as in the true background medium.
The divergence of the total stress field in the true medium is then:
| |
(56) |
The body force equivalent ![]() with respect to
with respect to ![]() is:
is:
| |
(57) |
Comparing (35) to (57) we see that
| |
(58) |
and since
| |
(59) |
the volumetric body force equivalent geometric reflection coefficient ![]() can be identified as
can be identified as
| |
(60) |
Finally, we calculate the scattered field ![]() in terms of the
geometric reflection coefficient
in terms of the
geometric reflection coefficient ![]() using (39), (57),
(45) and (40):
using (39), (57),
(45) and (40):
| |
(61) |
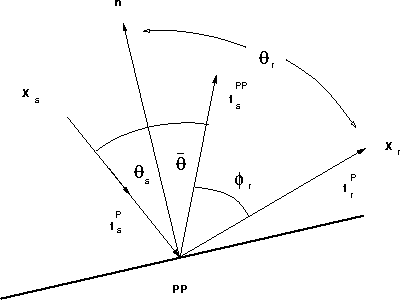
For clarity, we define the angles shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) :
:
| |
(62) |
| |
(63) |
| |
(64) |
and
| |
(65) |
 |
With these definitions, (61) can be written in compact form as:
| |
(66) |
To recap (66), the density at a
subsurface point is denoted ![]() , and the geometric reflection coefficient
at that point is
, and the geometric reflection coefficient
at that point is ![]() . The amplitude terms As and Ar represent
the cumulative geometric spreading, transmission loss, Q-attenuation, etc.,
from the source and receiver to the subsurface point
. The amplitude terms As and Ar represent
the cumulative geometric spreading, transmission loss, Q-attenuation, etc.,
from the source and receiver to the subsurface point ![]() respectively.
The factor Ar also includes the vector component projection at the surface
location
respectively.
The factor Ar also includes the vector component projection at the surface
location ![]() as defined by (42) and (43).
The term
as defined by (42) and (43).
The term ![]() is the total traveltime from source at
is the total traveltime from source at ![]() to the
subsurface point
to the
subsurface point ![]() and back up to the receiver at
and back up to the receiver at ![]() .Finally, the diffraction weight
.Finally, the diffraction weight ![]() represents the angle between the anticipated geometric specular reflection
direction
represents the angle between the anticipated geometric specular reflection
direction ![]() and the actual diffraction direction
and the actual diffraction direction ![]() . In the case
of specular reflection when
. In the case
of specular reflection when ![]() ,
, ![]() and so
and so ![]() .
.
We now make some general comments about the forward modeling theory given by (66).
This completes the forward modeling theory part of our paper that is necessary to proceed onward to the inverse estimation problem.