




Next: Interpolation in Stolt migration
Up: Popovici, Blondel, & Muir:
Previous: Popovici, Blondel, & Muir:
Downward continuation and imaging in the isotropic
case (Gazdag, 1978) can be written as
| 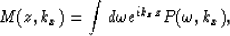 |
(1) |
where
| 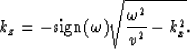 |
(2) |
In equation (1), 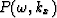 represents the
Fourier transform of the seismic field p(t,x) recorded at
the surface, following Claerbout's (1985) sign convention
represents the
Fourier transform of the seismic field p(t,x) recorded at
the surface, following Claerbout's (1985) sign convention
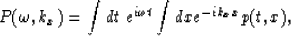
and v represents half the velocity, as
used in the exploding reflectors model.
We can rewrite equation (1) as time migration replacing
the depth steps by equivalent time steps  :
:
| 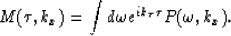 |
(3) |
where we define
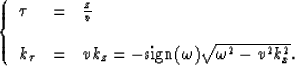
For a constant velocity medium, Stolt (1978) transforms the integral
in 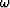 using a Fourier transform, which can be computed rapidly
via a Fast Fourier Transform (FFT) algorithm
using a Fourier transform, which can be computed rapidly
via a Fast Fourier Transform (FFT) algorithm
| 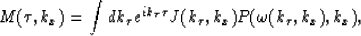 |
(4) |
where 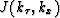 represents the Jacobian of the transformation
from
represents the Jacobian of the transformation
from 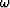 to
to 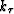
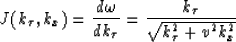
and 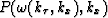 represents the initial data
as function of the new variable
represents the initial data
as function of the new variable 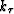 .
.





Next: Interpolation in Stolt migration
Up: Popovici, Blondel, & Muir:
Previous: Popovici, Blondel, & Muir:
Stanford Exploration Project
11/16/1997
![]()
![]() :
:
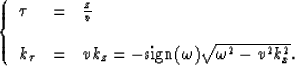
![]() using a Fourier transform, which can be computed rapidly
via a Fast Fourier Transform (FFT) algorithm
using a Fourier transform, which can be computed rapidly
via a Fast Fourier Transform (FFT) algorithm
![]()