




Next: The new interpolator
Up: INTRODUCTION
Previous: INTRODUCTION
Depending on the method used to transform
the field 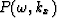 into the interpolated field
into the interpolated field
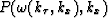 , different artifacts can
be introduced in the migrated image (Harlan, 1982; Ronen, 1982).
One way to eliminate the interpolation and
avoid artifacts in the migrated image is to
perform a slow Fourier transform in time with irregular values in
, different artifacts can
be introduced in the migrated image (Harlan, 1982; Ronen, 1982).
One way to eliminate the interpolation and
avoid artifacts in the migrated image is to
perform a slow Fourier transform in time with irregular values in
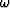 , but regular in
, but regular in 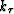 :
:
| 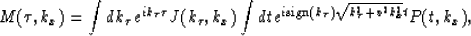 |
(5) |
where 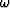 was replaced by
was replaced by
| 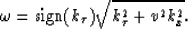 |
(6) |
Actually such an algorithm can be very appealing when implemented
on a parallel computer (Blondel, 1993) due to the high
degree of parallelism, and can run faster than the sequence
of FFT followed by interpolation.
The mapping function from 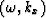 space to
space to
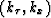 can be any anisotropic dispersion relation.
Dellinger et al. (1990) and Ecker and Muir (1993) show
examples of anisotropic migration operators by modifying the dispersion
relation (2).
can be any anisotropic dispersion relation.
Dellinger et al. (1990) and Ecker and Muir (1993) show
examples of anisotropic migration operators by modifying the dispersion
relation (2).
By comparing the standard Stolt migration with the
slow Fourier transform Stolt migration, we can deduce an interpolation
scheme that, when used in connection with the standard algorithm,
will be equivalent to the slower but more correct one.
In matrix format, we can write the slow Fourier FFT for a single
wavenumber kx as:
| ![\begin{displaymath}
M(k_{\tau};k_x)=
\left[
\begin{array}
{c}
P(\omega_1;k_x) ...
...\ P(t_2;k_x) \\ \vdots \\ P(t_n;k_x) \\ \end{array}\right].\end{displaymath}](img18.gif) |
(7) |
The variable 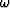 is not evenly sampled as required by the FFT.
Each
is not evenly sampled as required by the FFT.
Each 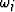 corresponds to an evenly sampled value of
corresponds to an evenly sampled value of 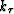 according to equation (6)
according to equation (6)
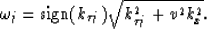
The ones in the slow FT matrix represent
zero values of time in the first column, i.e. t1=0.
We can multiply the data by a unit matrix composed from a forward FFT and
an inverse FFT before performing the slow FT
| ![\begin{displaymath}
\left[ P(\omega_i;k_x) \right ] =
\left[ SFT \right]
\left[ FFT^{-1} \right] \left[ FFT \right]
\left[ P(t_i;k_x) \right].\end{displaymath}](img21.gif) |
(8) |
We observe that by combining the operations
| ![\begin{displaymath}
\left[ SFT \right]
\left[ FFT^{-1} \right]\end{displaymath}](img22.gif) |
(9) |
and calling it interpolation, we obtain the classic Stolt migration
algorithm. What is left now is to identify exactly what
our interpolation is doing.





Next: The new interpolator
Up: INTRODUCTION
Previous: INTRODUCTION
Stanford Exploration Project
11/16/1997
![\begin{displaymath}
M(k_{\tau};k_x)=
\left[
\begin{array}
{c}
P(\omega_1;k_x) ...
...\ P(t_2;k_x) \\ \vdots \\ P(t_n;k_x) \\ \end{array}\right].\end{displaymath}](img18.gif)
![]()