The velocity operator

For the velocity operator V we use Newton's equations stating that the time rate of momentum change is the external momentum source minus the pressure gradient.

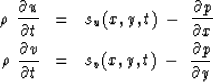
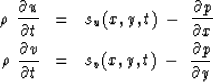$$\begin{eqnarray} \rho \ {\partial u \over \partial t} &=& s_u(x,y,t) \ -\ {\part... ...over \partial t} &=& s_v(x,y,t) \ -\ {\partial p \over \partial y}\end{eqnarray}$$ (15) (16)

The spatial tiling we have chosen gives us two independent locations for storing density $\rho$,one atop the horizontal velocity u, the other atop the vertical velocity v. It may seem non physical to have one density for vertical accelerations and another for horizontal ones, but it is worth maintaining the two densities as separate entities. Waves arise from many physical paradigms besides the acoustical one and some of these may require that we maintain this possibility to introduce anisotropy. Another way to introduce anisotropy in the present codes is to have two compressibilities K in the pressure subroutine. These extra parameters might also be helpful if we were trying to improve the numerical representation of the differential operators. Subroutine velocity() uses rhou(,) for $\Delta t/(\Delta x \rho)$ at u and rhov(,) for $\Delta t/(\Delta x \rho)$ at v. Equation (15) in discrete form  

$$u_{t+1}^x \quad =\quad s_t^x + u_t^x - \rho_u^{-1} (\Delta t/ \Delta x) (p_t^{x+1,y}-p_t^{x,y})$$ (17)

appears in subroutine velocity() at the line beginning with r(x,y,u)=.

# Operator of momentum change from gradient of pressure
#
subroutine velocity( adj, add, rhou,rhov,  q,nx,ny,    r )
integer              adj, add,               nx,ny,       x, y,  p,   u,   v
real rhou(nx,ny), rhov(nx,ny), q(nx,ny,3), r(nx,ny,3)
call        adjnull( adj, add,             q,nx*ny*3,  r,nx*ny*3)
							        p=1; u=2; v=3
do x= 2, nx-1 {
do y= 2, ny-1 {
    if( adj == 0) {
	r(x,y,u)= r(x,y,u) + q(x,y,u) - ( q(x+1,y  ,p) - q(x,y,p)) * rhou(x,y)
	r(x,y,v)= r(x,y,v) + q(x,y,v) - ( q(x  ,y+1,p) - q(x,y,p)) * rhov(x,y)
	r(x,y,p)= r(x,y,p) + q(x,y,p)		
    } else {
	q(x  ,y  ,u)= q(x  ,y  ,u) + r(x,y,u)
	q(x  ,y  ,p)= q(x  ,y  ,p) + r(x,y,u) * rhou(x,y) + r(x,y,p)
	q(x+1,y  ,p)= q(x+1,y  ,p) - r(x,y,u) * rhou(x,y)
	#       
	q(x  ,y  ,v)= q(x  ,y  ,v) + r(x,y,v)
	q(x  ,y  ,p)= q(x  ,y  ,p) + r(x,y,v) * rhov(x,y)
	q(x  ,y+1,p)= q(x  ,y+1,p) - r(x,y,v) * rhov(x,y)
	}
    }}
return; end

This time we pass through the pressure unchanged so we also see an added pressure term in the adjoint.