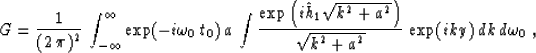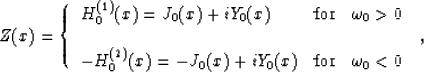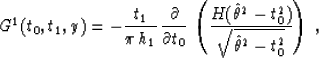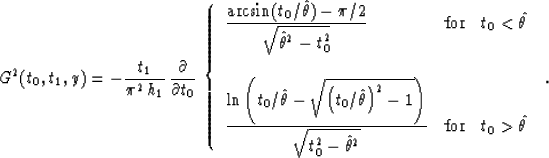Next: About this document ...
Up: Fomel: Offset continuation
Previous: THE KINEMATICS OF OFFSET
The purpose of this appendix is to explain the apparent difference
between Hale's DMO operator Hale (1984) and operator (17), which
is the first term in the offset continuation to zero offset. The
difference between the two operators is simply the real part of Hale's
DMO. Therefore, I will analyze the real and the imaginary part
separately and discuss the contributions of each. In order to
do this, I derive the impulse response of Hale's DMO in the
time-and-space domain, following the results of Stovas and Fomel
1993. The high-frequency asymptotics of the impulse
response has been investigated previously in a number of publications
Berg (1985); Hale (1991a); Liner (1990). Here we will obtain
an exact formula, containing both high-frequency and low-frequency
components.
Starting from Hale's DMO operator Hale (1984)
| 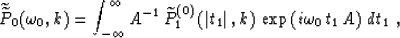 |
(74) |
let us define its impulse response as a function G(t0,t1,y) such
that
| 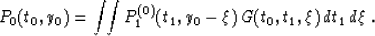 |
(75) |
According to this definition, the impulse response of operator (77)
can be expressed as
| 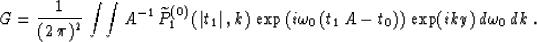 |
(76) |
Recalling the definition of Hale's factor A (19) and changing the
order of integration in the double integral, we can then rewrite expression
(79) to the form
| 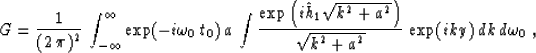 |
(77) |
where 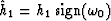 , and
, and
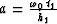 .
.
The inner integral in (80) is a known definite integral, evaluated
explicitly in terms of cylinder functions Gradshtein and Ryzhik (1994). The idea of applying
cylinder functions to the evaluation of the DMO impulse response was
used previously by Berg 1985 and Hale
1991a. After evaluation of the inner integral,
expression (80) transforms to
| 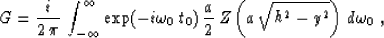 |
(78) |
where
| 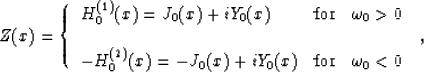 |
(79) |
H0(1) and H0(2) are Hankel functions of zero order, and
J0 and Y0 are, respectively, Bessel function and Weber function of zero
order. Separating the real and the imaginary parts of the integrand
transforms expression (81) to the form
| ![\begin{displaymath}
\left. +\int_0^{\infty}
\sin(\omega_0\,t_0)\,
Y_0\left(\omega_0\,\hat{\theta}\right)\,
d\omega_0 \right]\;,\end{displaymath}](img145.gif) |
(80) |
where
| 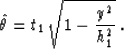 |
(81) |
Note that the Bessel function in the first term of formula
(83) follows from the real part of the Hankel function, which
is in turn connected with the imaginary part of Hale's operator
(77). For the same reason, the second term in formula
(83) is the contribution from the real part of operator
(77). Both definite integrals in (83) have known
analytical expressions listed in integral tables Gradshtein and Ryzhik (1994). With
the help of these expressions, the first term is expressed as
| 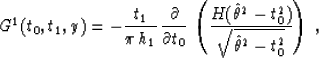 |
(82) |
while the second term transforms to
| 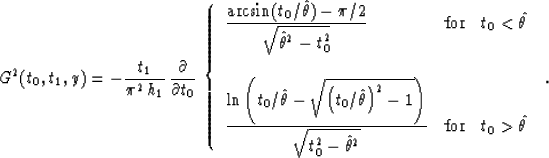 |
(83) |
The first term (G1) is discontinuous on the line
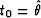 , which is the known form of the DMO impulse response
Deregowski and Rocca (1981), while the second term (G2) is continuous and
smooth everywhere. In order to prove this fact, one can easily verify that
both the left-sided and right-sided limits of expression (86) for
t0 approaching
, which is the known form of the DMO impulse response
Deregowski and Rocca (1981), while the second term (G2) is continuous and
smooth everywhere. In order to prove this fact, one can easily verify that
both the left-sided and right-sided limits of expression (86) for
t0 approaching 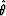 are
are
| 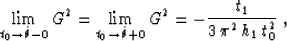 |
(84) |
and the limits of its derivative are
| 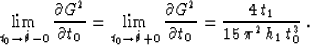 |
(85) |
The second (smooth) term of the impulse response, which comes from
the real part of Hale's DMO, obviously does not contribute to the imaging
properties of DMO. Moreover, it continues non-causally
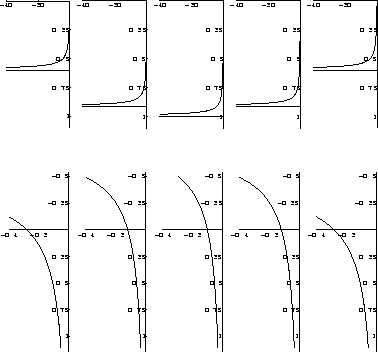
(and with monotonical growth) to the negative times (Figure
7), which contradicts the sense of DMO (and offset
continuation) as an operator defined for positive times only. The
energy of the second term is almost negligible, especially with
respect to the high-frequency asymptotics. Therefore, in practice its
presence doesn't affect the DMO behavior much. The conclusion that is
made in this Appendix justifies the absence of this term in the DMO
operator derived from the amplitude-preserving offset continuation
(17).
offimp
Figure 7
Theoretical impulse response of Hale's DMO. Top: impulse response of
the imaginary part; bottom: impulse response of the real part.
Note the scale difference.










Next: About this document ...
Up: Fomel: Offset continuation
Previous: THE KINEMATICS OF OFFSET
Stanford Exploration Project
11/12/1997