




Next: Kinematics of Zero-Offset Velocity
Up: Fomel: Velocity continuation
Previous: Introduction
From the kinematic point of view, it is convenient to describe the
reflector as a locally smooth surface z = z(x), where z is the
depth, and x is the point on the surface (x is a two-dimensional
vector in the 3-D problem). The image of the reflector obtained after
a common-offset prestack migration with a half-offset h and a
constant velocity v is the surface z = z(x;h,v). Appendix A
provides the derivations of the partial differential equation
describing the image surface in the depth-midpoint-offset-velocity
space. The purpose of this section is to discuss the laws of kinematic
transformations implied by the velocity continuation equation. Later
in this paper, I obtain dynamic analogues of the kinematic
relationships in order to describe continuation of migrated sections in the velocity space.
The kinematic equation for prestack velocity continuation, derived in
Appendix A, takes the following form:
| 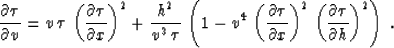 |
(1) |
Here  denotes the one-way vertical traveltime
denotes the one-way vertical traveltime 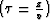 . The right-hand side of equation (1)
consists of three distinctive terms. Each has its own geophysical meaning. The first term is the only one remaining
when the offset h equals zero. It corresponds to the procedure of
zero-offset residual migration. Setting the reflector dip to
zero eliminates the first and third terms, leaving the second,
dip-independent one. We can associate the second term with the process of
residual normal moveout. The third term is both dip- and offset-
dependent. The process that it describes is residual dip
moveout. It is convenient to analyze each of the three processes
separately, evaluating their contributions to the cumulative process
of prestack velocity continuation.
. The right-hand side of equation (1)
consists of three distinctive terms. Each has its own geophysical meaning. The first term is the only one remaining
when the offset h equals zero. It corresponds to the procedure of
zero-offset residual migration. Setting the reflector dip to
zero eliminates the first and third terms, leaving the second,
dip-independent one. We can associate the second term with the process of
residual normal moveout. The third term is both dip- and offset-
dependent. The process that it describes is residual dip
moveout. It is convenient to analyze each of the three processes
separately, evaluating their contributions to the cumulative process
of prestack velocity continuation.





Next: Kinematics of Zero-Offset Velocity
Up: Fomel: Velocity continuation
Previous: Introduction
Stanford Exploration Project
11/12/1997