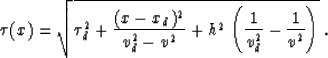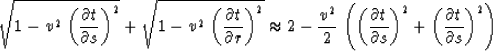Next: Kinematics of Residual DMO
Up: KINEMATICS OF VELOCITY CONTINUATION
Previous: Kinematics of Zero-Offset Velocity
The residual NMO differential equation is the second term in
(1):
| 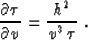 |
(22) |
Equation (22) is independent from the midpoint
x. This fact indicates the one-dimensional nature of normal
moveout. The general solution of equation (22) is
obtained by simple integration. It takes the form
| 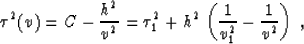 |
(23) |
where C is an arbitrary velocity-independent constant, and I have
chosen the constants 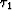 and v1 so that
and v1 so that 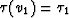 .
.
For the case of a point diffractor, solution (23) easily
combines with the zero-offset solution (16). The result is a
simplified version of the prestack residual migration summation path:
| 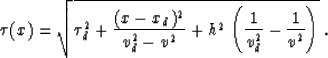 |
(24) |
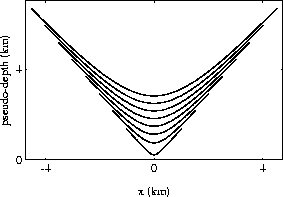
Summation paths of the form (24) for a set of diffractors
with different depths are plotted in Figures 3 and
4. The parameters chosen in these plots allow a direct
comparison with Etgen's Figures 2.4 and 2.5 Etgen (1990),
based on the exact solution and reproduced in Figures 9 and
10. The comparison shows that the approximate
solution (24) captures the main features of the prestack
residual migration operator, except for the residual DMO cusps
appearing in the exact solution when the diffractor depth is smaller
than the offset.
vlcve1
Figure 3 Summation paths of the
simplified prestack residual migration for a series of depth
diffractors. Residual slowness v/vd is 1.2; offset h is 1
km. This figure is to be compared with Etgen's Figure 2.4.
|
| 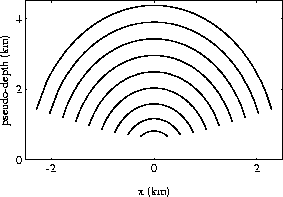 |





vlcve2
Figure 4 Summation paths of the simplified
prestack residual migration for a series of depth diffractors. Residual
slowness v/vd is 0.8; offset h is 1 km. This figure is to be
compared with Etgen's Figure 2.5.
|
|  |





Neglecting the residual DMO term in residual migration is
approximately equivalent in accuracy to neglecting the DMO step in
conventional processing. Indeed, as follows from the geometric analogue
of equation (1) derived in Appendix A, dropping the residual
DMO term corresponds to the condition
| 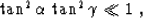 |
(25) |
where  is the dip angle, and
is the dip angle, and 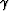 is the reflection angle.
As shown by Yilmaz and Claerbout 1980, the
conventional processing sequence without the DMO step corresponds to
the separable approximation of the double-square-root equation (67):
is the reflection angle.
As shown by Yilmaz and Claerbout 1980, the
conventional processing sequence without the DMO step corresponds to
the separable approximation of the double-square-root equation (67):
| 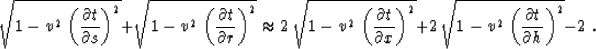 |
(26) |
In geometric terms, approximation (26) transforms to
| 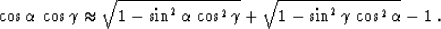 |
(27) |
Estimating the accuracy of the separable approximation by the
first term of the Taylor series for small  and
and 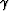 yields
the estimate of
yields
the estimate of 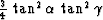 Yilmaz and Claerbout (1980), which agrees qualitatively with
(25). Though approximation (24) fails in
situations where the dip moveout correction is necessary, it is
significantly more accurate than the 15-degree approximation of the
double-square-root equation, implied in the migration velocity
analysis method of Yilmaz and Chambers 1984
and MacKay and Abma 1992. The 15-degree approximation
Yilmaz and Claerbout (1980), which agrees qualitatively with
(25). Though approximation (24) fails in
situations where the dip moveout correction is necessary, it is
significantly more accurate than the 15-degree approximation of the
double-square-root equation, implied in the migration velocity
analysis method of Yilmaz and Chambers 1984
and MacKay and Abma 1992. The 15-degree approximation
| 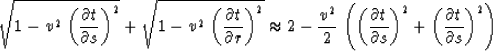 |
(28) |
corresponds geometrically to the equation
| 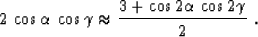 |
(29) |
Its estimated accuracy is 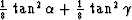 . Unlike the separable approximation, which is
accurate separately for zero offset and zero dip, the 15-degree
approximation fails at zero offset in the case of a steep dip and at zero
dip in the case of a large offset.
. Unlike the separable approximation, which is
accurate separately for zero offset and zero dip, the 15-degree
approximation fails at zero offset in the case of a steep dip and at zero
dip in the case of a large offset.





Next: Kinematics of Residual DMO
Up: KINEMATICS OF VELOCITY CONTINUATION
Previous: Kinematics of Zero-Offset Velocity
Stanford Exploration Project
11/12/1997