




Next: Velocity-Independent DMO
Up: Bednar: EOM vs. DMO-PSI
Previous: Introduction
In the early 1980's G. H. F. Gardner and colleagues at the
University of Houston showed that it was possible to DMO-correct
recorded data in a velocity-independent manner. The fundamental basis for
Gardner's method for velocity-independent DMO is the recognition
that the double-square-root equation can be converted into a single-square-root
equation by a radial-plane-diffraction process.
After application of DMO, a second diffraction process, which takes place on
constant time-slices completes the prestack migration step.
Consider a constant velocity medium with velocity v.
With reference to Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , the double-square root (DSR) equation
is:
, the double-square root (DSR) equation
is:
| 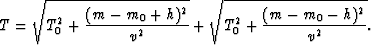 |
(1) |
Here m is the midpoint between source S and receiver R,
m0 is the arbitrary location of a fixed scatter point,
h is the half-offset,
T0 is the one-way zero-offset traveltime from the normal to the constant-time ellipse
at (x = (m - m0),y) to b, and T is the time required to traverse the path SPR.
Note that in this case, both m0 and m are referenced to the same fixed origin
while x = m - m0 is relative to m.
Fig1
Figure 1 Depth section showing constant-time ellipse for the DSR equation.

The ellipse in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is the locus of all points (x,y) for which T
is constant. It will be convenient to write (1) in the form:
is the locus of all points (x,y) for which T
is constant. It will be convenient to write (1) in the form:
| 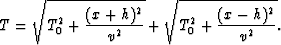 |
(2) |
Following Forel and Gardner (1988), let
| 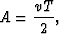 |
(3) |
and
| 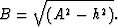 |
(4) |
Then
| 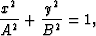 |
(5) |
| 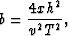 |
(6) |
and the distance from b to P satisfies
| 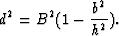 |
(7) |
Since
| 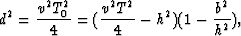 |
(8) |
one has
| 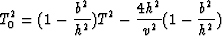 |
(9) |
This is the basic result from which DMO will be derived.





Next: Velocity-Independent DMO
Up: Bednar: EOM vs. DMO-PSI
Previous: Introduction
Stanford Exploration Project
10/10/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , the double-square root (DSR) equation
is:
, the double-square root (DSR) equation
is:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , the double-square root (DSR) equation
is:
, the double-square root (DSR) equation
is:
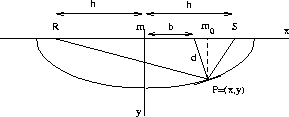
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) is the locus of all points (x,y) for which T
is constant. It will be convenient to write (1) in the form:
is the locus of all points (x,y) for which T
is constant. It will be convenient to write (1) in the form: