Next: Velocity-Independent-Prestack Imaging
Up: Bednar: EOM vs. DMO-PSI
Previous: The Velocity Independent DMO
Now define a new offset hg and time T1, as follows:
and
| 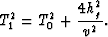 |
(11) |
Then after rearranging (9), one has
| 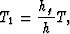 |
(12) |
Equations (10), (11), and (12) define
velocity-independent DMO. They
provide the framework for mapping traces with offset h and
midpont m to zero-offset traces with offset hg and midpoint m + b.
Note that this process requires no velocity information and
can be accomplished by a careful sampling or ``binning'' of b Gardner (1993).
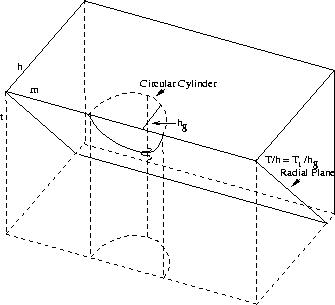
The trajectory of a single time sample T for a trace with
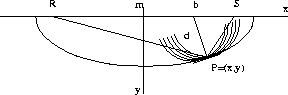
half-offset h in the new offset space hg is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
Fig2
.
Fig2
Figure 2 Radial-plane DMO.

Each fixed sample in (m,h,t) space is mapped to
a curve in (m+b,hg,t) space. Here, the curve lies in a radial
plane, within the data volume (m,h,t), defined by 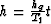 . It is
possible to show Gardner (1993) that the mapping can be accomplished by (f,k) migration
of the radial-plane data with the "velocity"
. It is
possible to show Gardner (1993) that the mapping can be accomplished by (f,k) migration
of the radial-plane data with the "velocity" 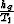 .Thus, the computational requirements for velocity-independent DMO are
.Thus, the computational requirements for velocity-independent DMO are 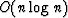 . Although
it is not within the scope of this article, Gardner 1993 also provides a
log-stretch-(f,k) version of this DMO when h (common-offset section) is fixed.
. Although
it is not within the scope of this article, Gardner 1993 also provides a
log-stretch-(f,k) version of this DMO when h (common-offset section) is fixed.
After DMO, the new output volume consists of zero-offset but
unmigrated data. Arrival times are specified by (11)
and as a result are completely hyperbolic functions of hg. The new data set can
be NMO corrected, and stacked, to produce a zero-offset section.
Any form of standard time migration may then be applied to
produce a proper subsurface image.
Note also that if each new equivalent offset is migrated after NMO but
prior to stack, then each point on the diffraction
curve of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) will result in one of the circles
indicated in Figure
will result in one of the circles
indicated in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . After stack, the envelope of the circles,
as also indicated in Figure
. After stack, the envelope of the circles,
as also indicated in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , will be the equal-traveltime ellipse
of (2). Since the radii of each of these circles is
given by the velocity-independent equation (7), one can postulate
that constant-velocity-prestack imaging requires no initial
velocity information.
, will be the equal-traveltime ellipse
of (2). Since the radii of each of these circles is
given by the velocity-independent equation (7), one can postulate
that constant-velocity-prestack imaging requires no initial
velocity information.
Fig3
Figure 3 Ellipse as envelope of circles.






Next: Velocity-Independent-Prestack Imaging
Up: Bednar: EOM vs. DMO-PSI
Previous: The Velocity Independent DMO
Stanford Exploration Project
10/10/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
![]() . It is
possible to show Gardner (1993) that the mapping can be accomplished by (f,k) migration
of the radial-plane data with the "velocity"
. It is
possible to show Gardner (1993) that the mapping can be accomplished by (f,k) migration
of the radial-plane data with the "velocity" ![]() .Thus, the computational requirements for velocity-independent DMO are
.Thus, the computational requirements for velocity-independent DMO are ![]() . Although
it is not within the scope of this article, Gardner 1993 also provides a
log-stretch-(f,k) version of this DMO when h (common-offset section) is fixed.
. Although
it is not within the scope of this article, Gardner 1993 also provides a
log-stretch-(f,k) version of this DMO when h (common-offset section) is fixed.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) will result in one of the circles
indicated in Figure
will result in one of the circles
indicated in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . After stack, the envelope of the circles,
as also indicated in Figure
. After stack, the envelope of the circles,
as also indicated in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , will be the equal-traveltime ellipse
of (2). Since the radii of each of these circles is
given by the velocity-independent equation (7), one can postulate
that constant-velocity-prestack imaging requires no initial
velocity information.
, will be the equal-traveltime ellipse
of (2). Since the radii of each of these circles is
given by the velocity-independent equation (7), one can postulate
that constant-velocity-prestack imaging requires no initial
velocity information.