Next: EQUIVALENT OFFSET MIGRATION
Up: Bednar: EOM vs. DMO-PSI
Previous: Velocity-Independent DMO
At this point in the analysis, application of velocity-independent
DMO has produced a volume with normal moveout given
by
| 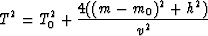 |
(13) |
Although one could, in principle, estimate v from this equation,
the value would be relative to the normal from m+b and not to the desired (migrated) location,
m0. To see what must be accomplished to migrate the DMO volume
let
|
h02 = (m - m0)2 + h2.
|
(14) |
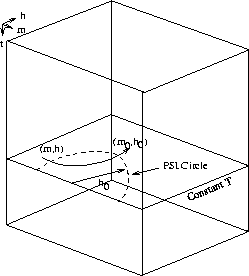
The volume will be focused after points on the circle with center (m0,0)
and radius h0 are mapped to the point (m0,h0). After focusing, the relation
between T, T0, h0, and v is given by
| 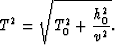 |
(15) |
Velocity-independent focusing requires that m0 and h0 be expressed in terms of m and h. First,
differentiate (13) with respect to m and h to get
| 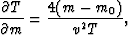 |
(16) |
| 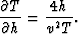 |
(17) |
Second, solve for the derivative of h with respect to m
| 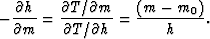 |
(18) |
Finally, rewrite (18) as
| 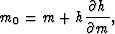 |
(19) |
and substitute (19) into (14) so that
| 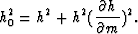 |
(20) |
Equations (19) and (20) define PSI. As illustrated in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
they transform constant T slices from variables (m,h) to variables (m0,h0). Clearly, there
is no velocity dependence, so PSI is also a velocity-independent process. As was the
case for DMO, PSI can also be formulated Gardner (1993) as an (f,k) process. In this case
the process is equivalent to (f,k) (Stolt) modeling rather than migration.
,
they transform constant T slices from variables (m,h) to variables (m0,h0). Clearly, there
is no velocity dependence, so PSI is also a velocity-independent process. As was the
case for DMO, PSI can also be formulated Gardner (1993) as an (f,k) process. In this case
the process is equivalent to (f,k) (Stolt) modeling rather than migration.
Fig4
Figure 4 Prestack imaging for constant slice T.






Next: EQUIVALENT OFFSET MIGRATION
Up: Bednar: EOM vs. DMO-PSI
Previous: Velocity-Independent DMO
Stanford Exploration Project
10/10/1997
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
they transform constant T slices from variables (m,h) to variables (m0,h0). Clearly, there
is no velocity dependence, so PSI is also a velocity-independent process. As was the
case for DMO, PSI can also be formulated Gardner (1993) as an (f,k) process. In this case
the process is equivalent to (f,k) (Stolt) modeling rather than migration.
,
they transform constant T slices from variables (m,h) to variables (m0,h0). Clearly, there
is no velocity dependence, so PSI is also a velocity-independent process. As was the
case for DMO, PSI can also be formulated Gardner (1993) as an (f,k) process. In this case
the process is equivalent to (f,k) (Stolt) modeling rather than migration.