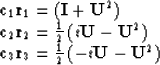Next: MATRIX FILTERS, SPECTRA, AND
Up: Matrices and multichannel time
Previous: REVIEW OF MATRICES
Sylvester's theorem provides a rapid way to calculate functions of a matrix.
Some simple functions of a matrix of frequent occurrence are
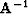 and
and 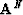 (for N large).
Two more matrix functions
which are very important in wave propagation
are
(for N large).
Two more matrix functions
which are very important in wave propagation
are 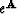 and
and 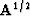 .Before going into the somewhat abstract proof of Sylvester's theorem,
we will take up a numerical example.
Consider the matrix
.Before going into the somewhat abstract proof of Sylvester's theorem,
we will take up a numerical example.
Consider the matrix
| ![\begin{displaymath}
{\bf A} \eq
\left[ \begin{array}
{rr}
3 & -2 \\ 1 & 0 \end{array} \right]\end{displaymath}](img49.gif) |
(26) |
It will be necessary to have the column eigenvectors and the eigenvalues of
this matrix; they are given by
| ![\begin{eqnarray}
\left[ \begin{array}
{rr}
3 & -2 \\ 1 & 0 \end{array} \right]...
...ght]
\eq 2\, \left[ \begin{array}
{c}
2 \\ 1 \end{array} \right]\end{eqnarray}](img50.gif) |
(27) |
| (28) |
Since the matrix A is not symmetric,
it has row eigenvectors which
differ from the column vectors.
These are
| ![\begin{eqnarray}
\left[-1 \quad 2\right] \,
\left[ \begin{array}
{rr}
3 & -2 \\...
... -2 \\ 1 & 0 \end{array} \right] &= & 2\, \left[1 \quad -1\right]\end{eqnarray}](img51.gif) |
(29) |
| (30) |
We may abbreviate equations (27) through (30) by
| 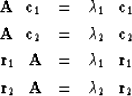 |
|
| |
| (31) |
| |
The reader will observe that r or c could be multiplied by an
arbitrary scale factor and (31) would still be valid.
The eigenvectors are said to be normalized if scale factors have been chosen
so that 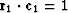 and
and 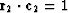 .It will be observed
that
.It will be observed
that 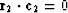 and
and 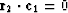 ,a general result to be established in the exercises.
,a general result to be established in the exercises.
Let us consider the behavior of the matrix 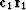 .
.
![\begin{displaymath}
{\bf c}_1 {\bf r}_1 \eq \left[
\begin{array}
{c}
1 \\ 1 \...
...
\left[ \begin{array}
{cc}
-1 & 2 \\ -1 & 2 \end{array} \right]\end{displaymath}](img58.gif)
Any power of this matrix is the matrix itself, for example its square.
![\begin{displaymath}
\left[ \begin{array}
{cc}
-1 & 2 \\ -1 & 2 \end{array} \righ...
... \left[ \begin{array}
{cc}
-1 & 2 \\ -1 & 2 \end{array} \right]\end{displaymath}](img59.gif)
This property is called idempotence (Latin for self-power).
It arises because
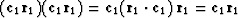 .The same thing is of course true of
.The same thing is of course true of
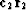 . Now notice that the matrix
. Now notice that the matrix
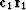 is ``perpendicular'' to the matrix
is ``perpendicular'' to the matrix
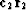 , that is
, that is
![\begin{displaymath}
\left[ \begin{array}
{cc}
2 & -2 \\ 1 & -1 \end{array} \righ...
...q \left[ \begin{array}
{cc}
0 & 0 \\ 0 & 0 \end{array} \right] \end{displaymath}](img62.gif)
since 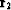 and
and 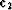 are perpendicular.
are perpendicular.
Sylvester's theorem says that any function f of the matrix A may be
written
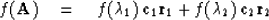
The simplest example is 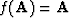
| ![\begin{eqnarray}
{\bf A} &= & \lambda_1 \, {\bf c}_1 {\bf r}_1 +
\lambda_2 \, {...
... \eq
\left[ \begin{array}
{rr}
3 & -2 \\ 1 & 0 \end{array} \right]\end{eqnarray}](img67.gif) |
|
| (32) |
Another example is
![\begin{displaymath}
A^2 \eq 1^2\,
\left[ \begin{array}
{cc}
-1 & 2 \\ -1 & 2 \e...
...
\left[ \begin{array}
{rr}
7 & -6 \\ 3 & -2 \end{array} \right]\end{displaymath}](img68.gif)
The inverse is
![\begin{displaymath}
A^{-1} \eq 1^{-1}\,
\left[ \begin{array}
{cc}
-1 & 2 \\ -1 ...
...,
\left[ \begin{array}
{rr}
0 & 2 \\ -1 & 3 \end{array} \right]\end{displaymath}](img69.gif)
The identity matrix may be expanded in terms of the eigenvectors of the
matrix A.
![\begin{displaymath}
A^0 \eq {\bf I} \eq 1^0\,
\left[ \begin{array}
{cc}
-1 & 2 ...
...eq
\left[ \begin{array}
{rr}
1 & 0 \\ 0 & 1 \end{array} \right]\end{displaymath}](img70.gif)
Before illustrating some more complicated functions let us see what it takes
to prove Sylvester's theorem.
We will need one basic result which is in all the books on matrix theory,
namely, that most matrices (see exercises) can be diagonalized.
In terms of our  example this takes the form
example this takes the form
| ![\begin{displaymath}
\left[ {{\bf r}_1 \over {\bf r}_2} \right] {\bf A}\, [{\bf c...
...array}
{cc}
\lambda_1 & 0 \\ 0 & \lambda_2 \end{array} \right]\end{displaymath}](img71.gif) |
(33) |
where
| ![\begin{displaymath}
\left[ {{\bf r}_1 \over {\bf r}_2} \right] \, [{\bf c}_1 \mi...
...q
\left[ \begin{array}
{cc}
1 & 0 \\ 0 & 1 \end{array} \right]\end{displaymath}](img72.gif) |
(34) |
Since a matrix commutes with its inverse, (34) implies
| ![\begin{displaymath}[{\bf c}_1 \mid {\bf c}_2]
\,
\left[ {{\bf r}_1 \over {\bf r...
...q
\left[ \begin{array}
{cc}
1 & 0 \\ 0 & 1 \end{array} \right]\end{displaymath}](img73.gif) |
(35) |
Postmultiply (33) by the row matrix
and premultiply by the column matrix.
Using (35),
we get
| ![\begin{displaymath}
{\bf A} \eq [{\bf c}_1 \mid {\bf c}_2]
\left[ \begin{array}...
...\end{array} \right]
\left[ {{\bf r}_1 \over {\bf r}_2} \right]\end{displaymath}](img74.gif) |
(36) |
Equation (36) is (32) in disguise,
as we can see by writing (36) as
Now to get 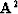 we have
we have
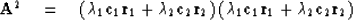
Using the orthonormality of 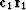 and
and 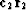 this reduces to
this reduces to
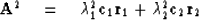
It is clear how (36) can be used to prove Sylvester's theorem
for any polynomial function of A.
Clearly, there is nothing peculiar about 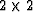 matrices either.
This works for
matrices either.
This works for 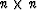 .Likewise, one may consider infinite series functions in A.
Since almost any function can be made up of infinite series,
we can consider also transcendental functions
like sine, cosine, exponential.
.Likewise, one may consider infinite series functions in A.
Since almost any function can be made up of infinite series,
we can consider also transcendental functions
like sine, cosine, exponential.
Exponentials arise naturally as the solutions to differential equations.
Consider the matrix differential equation
| 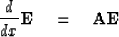 |
(37) |
One may readily verify the power series solution
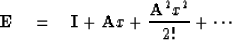
This is the power series definition of an exponential function.
If the matrix A is one of that vast majority which can be diagonalized,
then the exponential can be more simply expressed by Sylvester's theorem.
For the numerical example we have been considering, we have
![\begin{displaymath}
{\bf E} \eq
e^x \, \left[
\begin{array}
{cc}
-1 & 2 \\ -1 &...
... \left[
\begin{array}
{cc}
2 & -2 \\ 1 & -1 \end{array} \right]\end{displaymath}](img81.gif)
The exponential matrix is a solution
to the differential equation (37) without regard to boundaries.
It frequently happens that physics gives one a differential equation
| ![\begin{displaymath}
{d \over dx} \,
\left[ \begin{array}
{c}
y_1 \\ y_2 \end{a...
...f A}\,
\left[ \begin{array}
{c}
y_1 \\ y_2 \end{array} \right]\end{displaymath}](img82.gif) |
(38) |
Subject to two boundary conditions on either of y1 or y2 or a
combination.
One may verify that
![\begin{displaymath}
\left[ \begin{array}
{c}
y_1 \\ y_2 \end{array} \right] \eq...
...}x} \,
\left[ \begin{array}
{c}
k_1 \\ k_2 \end{array} \right]\end{displaymath}](img83.gif)
is the solution to (38) for arbitrary constants k1 and k2.
Boundary conditions are then used to determine
the numerical values of k1 and k2.
Note that k1 and k2 are just y2 (x = 0) and y2 (x = 0).
An interesting situation arises with the square root of a matrix.
A 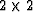 matrix like A will have four square roots
because there are four possible combinations for choice
of plus or minus signs on
matrix like A will have four square roots
because there are four possible combinations for choice
of plus or minus signs on 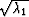 and
and 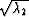 .In general, an
.In general, an 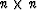 matrix has 2n square roots.
An important application arises in a later chapter,
where we will deal with the differential operator
matrix has 2n square roots.
An important application arises in a later chapter,
where we will deal with the differential operator
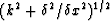 .The square root of an operator is explained in very few books and few people
even know what it means.
The best way to visualize the square root of this differential operator
is to relate it to the square root of the matrix M
where
.The square root of an operator is explained in very few books and few people
even know what it means.
The best way to visualize the square root of this differential operator
is to relate it to the square root of the matrix M
where
![\begin{displaymath}
{\bf M} \eq k^2 \,
\left[ \begin{array}
{ccccc}
1 & && & \\...
...-2 & 1 & \\ && 1 & -2 & 1 \\ & & & ? & ? \end{array} \right] \end{displaymath}](img87.gif)
The right-hand matrix is a second difference approximation
to a second partial derivative.
Let us define

Clearly we wish to consider M generalized to a very large size so that
the end effects may be minimized.
In concept, we can make M as large
as we like and for any size we can get 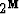 square roots.
In practice there will be only two square roots of interest,
one with the plus roots of all the eigenvalues
and the other with all the minus roots.
How can we find these ``principal value'' square roots?
An important case of interest is where we can use the binomial theorem so that
The result is justified by merely squaring the assumed square root.
Alternatively, it may be justified by means of Sylvester's theorem.
It should be noted that on squaring the assumed square root
one utilizes the fact that I and T commute.
We are led to the idea that the square root of
the differential operator may be interpreted as
square roots.
In practice there will be only two square roots of interest,
one with the plus roots of all the eigenvalues
and the other with all the minus roots.
How can we find these ``principal value'' square roots?
An important case of interest is where we can use the binomial theorem so that
The result is justified by merely squaring the assumed square root.
Alternatively, it may be justified by means of Sylvester's theorem.
It should be noted that on squaring the assumed square root
one utilizes the fact that I and T commute.
We are led to the idea that the square root of
the differential operator may be interpreted as
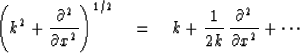
provided that k is not a function of x.
If k is a function of x,
the square root of the differential operator still has meaning but is not
so simply computed with the binomial theorem.
EXERCISES:
- Premultiply (31)b by
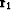 and postmultiply
(31)c by
and postmultiply
(31)c by 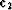 ,then subtract.
Is
,then subtract.
Is 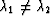 a necessary condition for
a necessary condition for 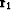 and
and 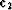 to be perpendicular?
Is it a sufficient condition?
to be perpendicular?
Is it a sufficient condition?
- Show the Cayley-Hamilton theorem, that is, if
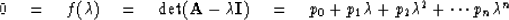
then
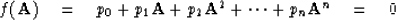
- Verify that, for a general
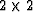 matrix A, for which
where
matrix A, for which
where 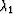 and
and 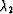 are eigenvalues of A. What is the
general form for
are eigenvalues of A. What is the
general form for 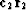 ?
?
- For a symmetric matrix it can be shown that there is always a complete
set of eigenvectors.
A problem sometimes arises with nonsymmetric matrices.
Study the matrix
![\begin{displaymath}
\left[
\begin{array}
{rc}
1 & 1 - \epsilon^2 \\ -1 & 3 \end{array} \right]\end{displaymath}](img99.gif)
as 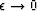 to see why one eigenvector is lost.
This is called a defective matrix.
(This example is from T. R. Madden.)
to see why one eigenvector is lost.
This is called a defective matrix.
(This example is from T. R. Madden.)
- A wide variety of wave-propagation problems in a stratified medium
reduce to the equation
![\begin{displaymath}
{d \over dx} \,
\left[ \begin{array}
{c}
y_1 \\ y_2 \end{...
...] \,
\left[ \begin{array}
{c}
y_1 \\ y_2 \end{array} \right] \end{displaymath}](img101.gif)
What is the x dependence of the solution when ab is positive?
When ab is negative?
Assume a and b are independent of x.
Use Sylvester's theorem.
What would it take to get a defective matrix?
What are the solutions in the case of a defective matrix?
- Consider a matrix of the form
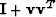 where v
is a column vector and
where v
is a column vector and 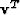 is its transpose.
Find
is its transpose.
Find 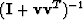 in terms of a power series in
in terms of a power series in 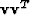 .[Note that
.[Note that 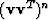 collapses to
collapses to 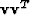 times a scaling factor,
so the power series reduces considerably.]
times a scaling factor,
so the power series reduces considerably.]
- The following ``cross-product'' matrix often arises in electrodynamics.
Let
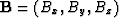
![\begin{displaymath}
U \eq {1 \over \sqrt{{\bf B} \cdot {\bf B}}} \,
\left[ \beg...
... & B_y \\ B_z & 0 & -B_x \\ -B_y & B_x & 0 \end{array} \right] \end{displaymath}](img108.gif)
- (a)
- Write out elements of
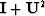 .
. - (b)
- Show that
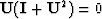 or
or
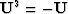 .
. - (c)
- Let
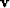 be an arbitrary vector. In what geometrical
directions do Uv,
be an arbitrary vector. In what geometrical
directions do Uv,
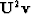 , and
, and 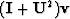 point?
point?
- (d)
- What are the eigenvalues of U?
[Hint: Use part (b).]
- (e)
- Why cannot U be canceled from
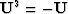 ?
?
- (f)
- Verify that the idempotent matrices of U are





Next: MATRIX FILTERS, SPECTRA, AND
Up: Matrices and multichannel time
Previous: REVIEW OF MATRICES
Stanford Exploration Project
10/30/1997
![]() and
and ![]() (for N large).
Two more matrix functions
which are very important in wave propagation
are
(for N large).
Two more matrix functions
which are very important in wave propagation
are ![]() and
and ![]() .Before going into the somewhat abstract proof of Sylvester's theorem,
we will take up a numerical example.
Consider the matrix
.Before going into the somewhat abstract proof of Sylvester's theorem,
we will take up a numerical example.
Consider the matrix
![\begin{eqnarray}
\left[ \begin{array}
{rr}
3 & -2 \\ 1 & 0 \end{array} \right]...
...ght]
\eq 2\, \left[ \begin{array}
{c}
2 \\ 1 \end{array} \right]\end{eqnarray}](img50.gif)
![\begin{eqnarray}
\left[-1 \quad 2\right] \,
\left[ \begin{array}
{rr}
3 & -2 \\...
... -2 \\ 1 & 0 \end{array} \right] &= & 2\, \left[1 \quad -1\right]\end{eqnarray}](img51.gif)
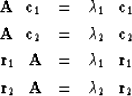
![]() .
.
![]()
![]()
![]()
![]()
![\begin{eqnarray}
{\bf A} &= & \lambda_1 \, {\bf c}_1 {\bf r}_1 +
\lambda_2 \, {...
... \eq
\left[ \begin{array}
{rr}
3 & -2 \\ 1 & 0 \end{array} \right]\end{eqnarray}](img67.gif)
![]()
![]()
![]()
![\begin{eqnarraystar}
{\bf A} &= &
[{\bf c}_1 \mid {\bf c}_2] \left\{
\left[ \be...
... \lambda_1 {\bf c}_1 {\bf r}_1 + \lambda_2 {\bf c}_2 {\bf r}_2\end{eqnarraystar}](img75.gif)
![]()
![]()
![]()
![]()
![]()
![]() matrix like A will have four square roots
because there are four possible combinations for choice
of plus or minus signs on
matrix like A will have four square roots
because there are four possible combinations for choice
of plus or minus signs on ![]() and
and ![]() .In general, an
.In general, an ![]() matrix has 2n square roots.
An important application arises in a later chapter,
where we will deal with the differential operator
matrix has 2n square roots.
An important application arises in a later chapter,
where we will deal with the differential operator
![]() .The square root of an operator is explained in very few books and few people
even know what it means.
The best way to visualize the square root of this differential operator
is to relate it to the square root of the matrix M
where
.The square root of an operator is explained in very few books and few people
even know what it means.
The best way to visualize the square root of this differential operator
is to relate it to the square root of the matrix M
where
![\begin{displaymath}
{\bf M} \eq k^2 \,
\left[ \begin{array}
{ccccc}
1 & && & \\...
...-2 & 1 & \\ && 1 & -2 & 1 \\ & & & ? & ? \end{array} \right] \end{displaymath}](img87.gif)
![]()
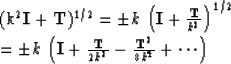
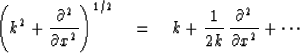
![]()
![]()
![]()
![]()
![\begin{displaymath}
U \eq {1 \over \sqrt{{\bf B} \cdot {\bf B}}} \,
\left[ \beg...
... & B_y \\ B_z & 0 & -B_x \\ -B_y & B_x & 0 \end{array} \right] \end{displaymath}](img108.gif)