




Next: BURG SPECTRAL ESTIMATION
Up: Waveform applications of least
Previous: Waveform applications of least
A data wavelet is given by b
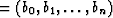 .We plan to construct a filter
f
.We plan to construct a filter
f 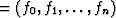 .Filtering is defined in this way:
When data b go into a filter f,
an output wavelet c is produced according
to the following matrix multiplication.
.Filtering is defined in this way:
When data b go into a filter f,
an output wavelet c is produced according
to the following matrix multiplication.
| ![\begin{displaymath}
\left[
\begin{array}
{l}
c_0 \\ c_1 \\ c_2 \\ \cdot \\ ...
...f_1 \\
\cdot \\ \cdot \\ \cdot \\ f_m \end{array} \right]\end{displaymath}](img3.gif) |
(1) |
This operation is often called
complete transient convolution.
It is the same as identifying
coefficients in a polynomial multiplication.
Now we introduce another wavelet
d which will have the same number of
components as c.
We call d the desired output of the filter.
We saw that c is the actual output.
The actual output c was seen to be a
function of the input b and the filter f.
The problem now is to determine f
so that c and d are very much alike.
Specifically we will choose
f so that the difference vector
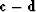 has minimum length squared
(in n + m + 1 dimensional space).
In other words,
we use the method of least squares to
solve the overdetermined equations
has minimum length squared
(in n + m + 1 dimensional space).
In other words,
we use the method of least squares to
solve the overdetermined equations
| ![\begin{displaymath}
\left[
\begin{array}
{llll}
b_0 & 0 & \cdots & 0 \\ b_1 & ...
...\cdot \\ \cdot \\ \cdot \\ d_{n+m} \\
\end{array} \right]\end{displaymath}](img5.gif) |
(2) |
Using the ``quick-and-dirty" method
of the previous chapter we merely premultiply
(2) by the transposed matrix.
The result is a Toeplitz matrix of the form
| ![\begin{displaymath}
\left[
\begin{array}
{lllll}
r_0 & r_1 & r_2 & \cdots & r_m...
...{l}
g_0 \\ g_1 \\ g_2 \\ \vdots \\ g_m \end{array} \right]\end{displaymath}](img6.gif) |
(3) |
where rk is the autocorrelation of
the input xk and gk
is a crosscorrelation of the input xk
with the desired output dk.
For computation techniques see Chapter 7.5.
The formulas of this section may also be used
to attempt to predict a time series from its past.
For example 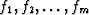 is a
prediction filter of xt+10 from
is a
prediction filter of xt+10 from
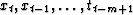 if we solve by least squares the equations
if we solve by least squares the equations
| ![\begin{displaymath}
\left[
\begin{array}
{l}
x_{10} \\ x_{11} \\ x_{12} \\ \...
...array}
{l}
f_1 \\ f_2 \\ \cdot \\ \cdot \end{array} \right]\end{displaymath}](img9.gif) |
(4) |
The matrix in (4) may be continued downward
for as far as one has data.
In an application,
the range of t in (4) would be over
past values of t. Then,
after solving the equations for the filter
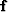 it would be hoped that the character
of the time series was such that
it would be hoped that the character
of the time series was such that 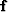 could
be used to predict future values of the time series
which had not gone into the equation defining
could
be used to predict future values of the time series
which had not gone into the equation defining 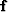 .
.
If the matrix of (4) is very much higher than it is wide,
it may be desirable to treat the end effects differently.
If one uses instead
| ![\begin{displaymath}
\left[
\begin{array}
{l}
x_{10} \\ x_{11} \\ \cdot \\ \c...
...[
\begin{array}
{l}
f_1 \\ \vdots \\ f_m \end{array} \right]\end{displaymath}](img11.gif) |
(5) |
one finds that the least-squares normal equation has a
Toeplitz matrix whereas for (4) the matrix in not Toeplitz.
As the reader is aware,
the Toeplitz matrix has many advantages,
both theoretical and computational.
Of special interest is the filter which is designed from the equations
| ![\begin{displaymath}
\left[
\begin{array}
{llll}
x_0 & & \multicolumn{2}{l}{\hbo...
...\\ \cdot \\ \cdot \\ \cdot \\ \\ \\ 0 \end{array} \right]\end{displaymath}](img12.gif) |
(6) |
Such a filter is called the
prediction error filter for unit span
because the ak operate on
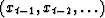 attempting to cancel xt.
Thus, the ak on the
attempting to cancel xt.
Thus, the ak on the 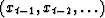 gives the negative of a best prediction of xt,
based on
gives the negative of a best prediction of xt,
based on 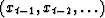 .The normal equations implied by (6)
are the square set
.The normal equations implied by (6)
are the square set
| ![\begin{displaymath}
\left[
\begin{array}
{lllc}
r_0 & r_1 & r_2 & \cdots \\ r_...
...{array}
{c}
v \\ 0 \\ 0 \\ \vdots \\ 0 \end{array} \right]\end{displaymath}](img14.gif) |
(7) |
It may be noted that the calculation of a prediction
error filter depends only on the autocorrelation of the
time series and not on the time series itself.
As we have seen (from (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )), the solutions to
these equations are coefficients of a minimum-phase polynomial.
)), the solutions to
these equations are coefficients of a minimum-phase polynomial.
Solutions to Toeplitz equations when the right-hand side
takes the more arbitrary form (3)
are not generally minimum-phase, but the Levinson recursion
may be generalized to make the calculation speedy.
This is done in Section 7.5 on the multichannel
Levinson recursion.
EXERCISES:
- Find a three-term zero delay inverse
to the wavelet (1,2). Compare the error to the error of
(2,1). Compare the waveform.
An extensive discussion of the error in least-squares
inverse filters is given in Reference 26.
One conclusion is that the sum of the squared errors
goes to zero as the filter length becomes infinite in
two situations:
(a) Zero delay inverse if and only if
the wavelet being inverted is minimum-phase.
(b) If the wavelet being inverted in not minimum-phase,
the error goes to zero only if the output is delayed,
that it, 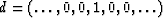 .Calculate a three-term delayed inverse to (1,2), that is,
try d = (0, 1, 0, 0) or d = (0, 0, 1, 0).
.Calculate a three-term delayed inverse to (1,2), that is,
try d = (0, 1, 0, 0) or d = (0, 0, 1, 0).
- A pressure sensor in a deep well records upgoing seismic
waves and, at some time t0 later,
identical downgoing waves of opposite sign.
Determine delayed and non-delayed least-squares
filters of length m to eliminate the double pulse.
(You should be able to guess the solution to large matrices
of this type. Try filters of the form
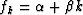 where
where  and
and 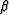 are scalars.) What is the error as a function of
the filter length?
are scalars.) What is the error as a function of
the filter length?
- Let
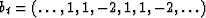 .Find by least squares the best one-term filter which
predicts bt, using only bt-1.
Find the best two-term filter using bt-1 and
bt-2. Likewise find the best three-term filter.
What is the error as a function of time in each case?
.Find by least squares the best one-term filter which
predicts bt, using only bt-1.
Find the best two-term filter using bt-1 and
bt-2. Likewise find the best three-term filter.
What is the error as a function of time in each case?





Next: BURG SPECTRAL ESTIMATION
Up: Waveform applications of least
Previous: Waveform applications of least
Stanford Exploration Project
10/30/1997
![\begin{displaymath}
\left[
\begin{array}
{l}
c_0 \\ c_1 \\ c_2 \\ \cdot \\ ...
...f_1 \\
\cdot \\ \cdot \\ \cdot \\ f_m \end{array} \right]\end{displaymath}](img3.gif)
![\begin{displaymath}
\left[
\begin{array}
{l}
c_0 \\ c_1 \\ c_2 \\ \cdot \\ ...
...f_1 \\
\cdot \\ \cdot \\ \cdot \\ f_m \end{array} \right]\end{displaymath}](img3.gif)
![]() has minimum length squared
(in n + m + 1 dimensional space).
In other words,
we use the method of least squares to
solve the overdetermined equations
has minimum length squared
(in n + m + 1 dimensional space).
In other words,
we use the method of least squares to
solve the overdetermined equations
![\begin{displaymath}
\left[
\begin{array}
{llll}
b_0 & 0 & \cdots & 0 \\ b_1 & ...
...\cdot \\ \cdot \\ \cdot \\ d_{n+m} \\
\end{array} \right]\end{displaymath}](img5.gif)
![\begin{displaymath}
\left[
\begin{array}
{lllll}
r_0 & r_1 & r_2 & \cdots & r_m...
...{l}
g_0 \\ g_1 \\ g_2 \\ \vdots \\ g_m \end{array} \right]\end{displaymath}](img6.gif)
![]() is a
prediction filter of xt+10 from
is a
prediction filter of xt+10 from
![]() if we solve by least squares the equations
if we solve by least squares the equations
![\begin{displaymath}
\left[
\begin{array}
{l}
x_{10} \\ x_{11} \\ x_{12} \\ \...
...array}
{l}
f_1 \\ f_2 \\ \cdot \\ \cdot \end{array} \right]\end{displaymath}](img9.gif)
![\begin{displaymath}
\left[
\begin{array}
{l}
x_{10} \\ x_{11} \\ \cdot \\ \c...
...[
\begin{array}
{l}
f_1 \\ \vdots \\ f_m \end{array} \right]\end{displaymath}](img11.gif)
![\begin{displaymath}
\left[
\begin{array}
{llll}
x_0 & & \multicolumn{2}{l}{\hbo...
...\\ \cdot \\ \cdot \\ \cdot \\ \\ \\ 0 \end{array} \right]\end{displaymath}](img12.gif)
![]() attempting to cancel xt.
Thus, the ak on the
attempting to cancel xt.
Thus, the ak on the ![]() gives the negative of a best prediction of xt,
based on
gives the negative of a best prediction of xt,
based on ![]() .The normal equations implied by (6)
are the square set
.The normal equations implied by (6)
are the square set
![\begin{displaymath}
\left[
\begin{array}
{lllc}
r_0 & r_1 & r_2 & \cdots \\ r_...
...{array}
{c}
v \\ 0 \\ 0 \\ \vdots \\ 0 \end{array} \right]\end{displaymath}](img14.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )), the solutions to
these equations are coefficients of a minimum-phase polynomial.
)), the solutions to
these equations are coefficients of a minimum-phase polynomial.
![]() .Calculate a three-term delayed inverse to (1,2), that is,
try d = (0, 1, 0, 0) or d = (0, 0, 1, 0).
.Calculate a three-term delayed inverse to (1,2), that is,
try d = (0, 1, 0, 0) or d = (0, 0, 1, 0).