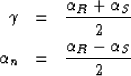Next: Analytical derivation
Up: REFERENCES
Previous: REFERENCES
To derive equation (2) we will change the coordinates system
in order to find the 2-D case illustrated in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -a) and
follow the derivation given in Fomel (1996).
-a) and
follow the derivation given in Fomel (1996).
geometry
Figure 8 a) 2-D geometry described by Sava and Fomel (2000). b) Common-azimuth formulation
of the problem. The derivation of equation (1) relies on the
definition of the problem into the propagation plane. Defined this way,
the 3-D problem becomes equivalent to the 2-D problem.
|
| 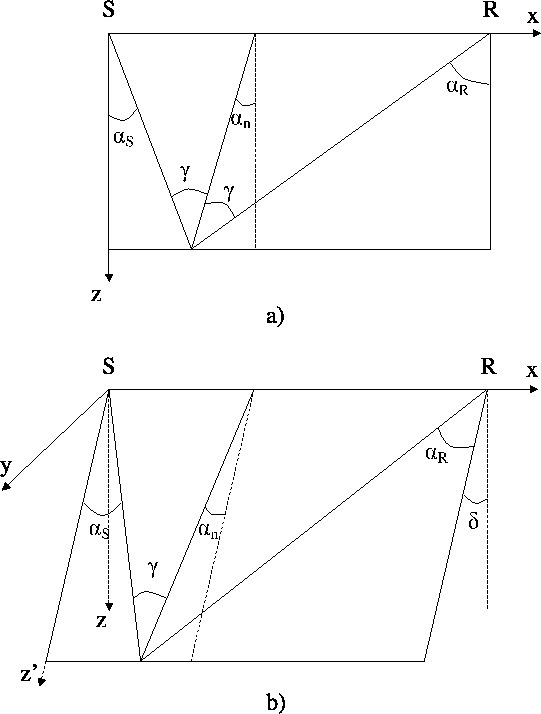 |

Consider the source and the receiver rays constrained to a slanted
propagation plane as illustrated in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -b).
The plane has dip angle
-b).
The plane has dip angle 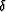 .Within the propagation plane, the source ray has a dip angle
.Within the propagation plane, the source ray has a dip angle
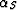 and the receiver ray a dip angle
and the receiver ray a dip angle 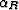 .We define z' as being a new vertical axis within the propagation plane:
the 3-D problem becomes a 2-D problem in this new basis.
The aperture angle
.We define z' as being a new vertical axis within the propagation plane:
the 3-D problem becomes a 2-D problem in this new basis.
The aperture angle 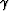 and the dipping angle
and the dipping angle 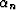 of the normal
of the interface at the reflection point can be expressed as a function
of
of the normal
of the interface at the reflection point can be expressed as a function
of 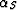 and
and 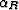 :
:
| 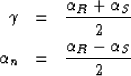 |
(8) |
| (9) |
The offset ray parameter in the propagation plane is:
| 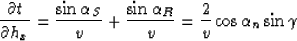 |
(10) |
We can write a 2-D version of the Double Square Root (DSR) in the
propagation plane:
| 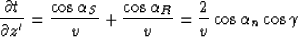 |
(11) |
The change of variable between the pseudo vertical axis z' and
the real vertical axis z is made with the
relation:
| 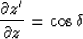 |
(12) |
With equations (11) and (12) the DSR expression in the
original coordinates system becomes:
| 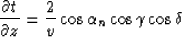 |
(13) |
The quotient of equations (10) and (13) leads to the expected
relation 2:
| 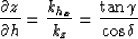 |
(14) |





Next: Analytical derivation
Up: REFERENCES
Previous: REFERENCES
Stanford Exploration Project
7/8/2003

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -a) and
follow the derivation given in Fomel (1996).
-a) and
follow the derivation given in Fomel (1996).