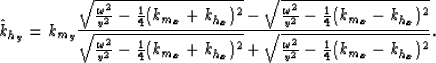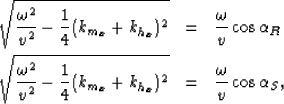Next: About this document ...
Up: REFERENCES
Previous: Geometrical derivation
Another way to find the relation between z and z' starts from
the cascade of two dispersion relations Biondi and Palacharla (1996).
The first one is for 2-D prestack downward-continuation along
the in-line direction,
| 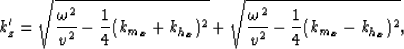 |
(15) |
which is equivalent to equation (11).
The second one is for 2-D zero-offset downward continuation along
the cross-line axis,
| 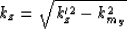 |
(16) |
which is equivalent to equation (12). Indeed, by taking
the square and dividing by kz,
| 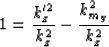 |
(17) |
and by introducing 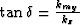 ,
,
| 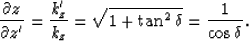 |
(18) |
BThe coplanarity condition presented in Biondi and Palacharla (1996) is:
| 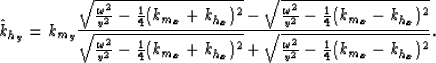 |
(19) |
Each square root in the previous equation can be substituted with the
expression including the dip angle of the source or the receiver ray
| 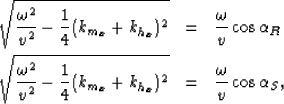 |
(20) |
| (21) |
where 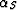 and
and 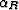 can be expressed in terms of the aperture
angle
can be expressed in terms of the aperture
angle 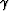 and the normal dip angle
and the normal dip angle 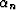 :
:
| 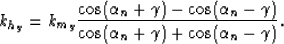 |
(22) |
Or, after applying some trigonometric relations
| 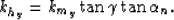 |
(23) |
We now introduce equation (2) as well as
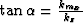 where
where
 is the projection of the angle
is the projection of the angle 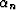 on the vertical plane
passing through the source-receiver axis.
The two angles are linked by the relation
on the vertical plane
passing through the source-receiver axis.
The two angles are linked by the relation
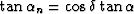 .Equation 23 becomes
.Equation 23 becomes
| 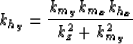 |
(24) |
CConsider one image point in the Fourier domain, i.e. at given
kmx, kmy and kz.
For one image point, we have all the values of the offset gather.
Each value is referenced in the Fourier domain by the offset wavenumbers
khx and khy.
Given a reflection azimuth 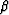 and an aperture angle
and an aperture angle 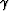 ,we want to get the value of the sample associated with
,we want to get the value of the sample associated with 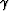 , hence
what are the offset wavenumbers associated with
, hence
what are the offset wavenumbers associated with 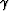 .Given kmx, kmy, kz,
.Given kmx, kmy, kz, 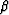 and
and 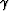 :
:
-
Because of the reflection azimuth, we need to get into the
new coordinates system. k'mx, k'my are computed using
kmx, kmy and
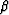 in equation (4).
in equation (4).
-
For a given
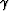 and kz we can determine k'hx from equation
(6).
and kz we can determine k'hx from equation
(6).
-
The second component of the offset wavenumber, k'hy, must satisfy
the coplanarity condition (7).
-
The two components of the offset wavenumber were obtained in the
new system of coordinates.
To return to the original system of coordinates, we use the inverse
of transformations (4).
-
We have determined which sample of the offset gather should
be associated with the aperture angle
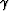 .
.
The entire angle gather at the image point (kmx, kmy, kz)
and at the reflection azimuth 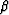 is obtained by looping over
is obtained by looping over
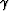 .
.





Next: About this document ...
Up: REFERENCES
Previous: Geometrical derivation
Stanford Exploration Project
7/8/2003