|
hyplay
Figure 2 Many hyperbolas tangent to a line. | 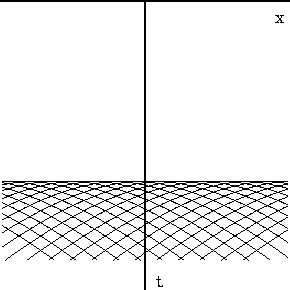 |
|
hyplay
Figure 2 Many hyperbolas tangent to a line. |  |
When a hyperbolic event carries a wavelet, the wavelet covers an area in the (t,x)-plane. Define this area as that between the two hyperbolas shown in Figure 3. These two curves are
| (5) | ||
| (6) |
|
hyparea
Figure 3 Detailed view of one of the many hyperbolas in figure 2. Two hyperbolas are separated by | 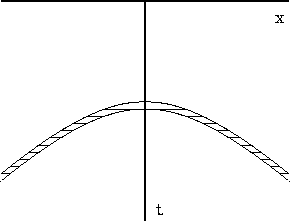 |
In the limit ![]() , the waveform is an impulse function
whose temporal spectrum is constant.
In that limit, the many waveforms in Figure 2
superpose giving a great concentration at the apex.
Since the many hyperbolas are identical with one another,
the time dependence of their sum is (within a scale factor)
the same time dependence of the shaded area of the single hyperbola
in Figure 3.
, the waveform is an impulse function
whose temporal spectrum is constant.
In that limit, the many waveforms in Figure 2
superpose giving a great concentration at the apex.
Since the many hyperbolas are identical with one another,
the time dependence of their sum is (within a scale factor)
the same time dependence of the shaded area of the single hyperbola
in Figure 3.
The separation between the two curves, ![]() is
is
| (7) |
| |
(8) |
By making this high frequency approximation,
we are setting aside some calculations
that we should be able to do for a constant velocity medium
but which would not apply to a medium with velocity as a function of depth.
Divergence considerations, for example,
suggest that the amplitude of each hyperbola should not be
a constant, but should drop off proportional to t-1/2.
Another example is that of parabolas instead
of hyperbolas, i.e. ![]() .(When velocity changes with depth, we no longer have hyperbolas,
but the tops of the traveltime curve could be approximated by a parabola.)
Then the amplitude is
.(When velocity changes with depth, we no longer have hyperbolas,
but the tops of the traveltime curve could be approximated by a parabola.)
Then the amplitude is ![]() .Notice that the divisor in equation (8) for the hyperbola
.Notice that the divisor in equation (8) for the hyperbola
![]() has the same half power discontinuity at z=tv as the parabola.
Thus the amplitude spectrum at high frequencies for either
the parabola or the hyperbola will drop off as the inverse
half power of frequency according to equation (2).
To get a plane wave with the constant spectrum of an impulse
instead of this inverse-square-root spectrum,
we must use hyperbolas (or parabolas),
not carrying an impulse function,
but instead carrying a square-root spectrum
(to cancel the inverse-square-root spectrum that arises
from superposing the hyperbolas).
Equation (4) gives us a causal waveform with the desired spectrum.
Thus the decomposition of an impulsive 2-D plane
wave into hyperbolas requires the hyperbolas to carry
the ``half-order differential'' waveform given in equation (4).
has the same half power discontinuity at z=tv as the parabola.
Thus the amplitude spectrum at high frequencies for either
the parabola or the hyperbola will drop off as the inverse
half power of frequency according to equation (2).
To get a plane wave with the constant spectrum of an impulse
instead of this inverse-square-root spectrum,
we must use hyperbolas (or parabolas),
not carrying an impulse function,
but instead carrying a square-root spectrum
(to cancel the inverse-square-root spectrum that arises
from superposing the hyperbolas).
Equation (4) gives us a causal waveform with the desired spectrum.
Thus the decomposition of an impulsive 2-D plane
wave into hyperbolas requires the hyperbolas to carry
the ``half-order differential'' waveform given in equation (4).