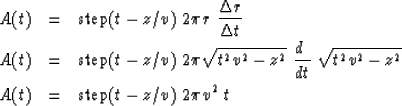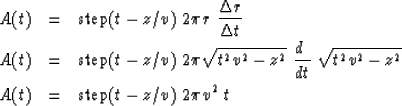Next: About this document ...
Up: Claerbout: Hankel tail
Previous: HUYGEN'S SECONDARY SOURCE IN
Interestingly,
the Huygen's wavelet is different in three dimensions
than in two dimensions.
In three dimensions, there is no Hankel tail.
In three dimensions we have the definition
x2+y2=r2 and
from t2v2=x2+y2+z2 we find on a plane of constant z,
that the equation for a circle expanding with time is
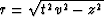 .Between time t and
.Between time t and 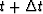 is a ring with an area
is a ring with an area
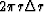 .Taking the signal amplitude in the ring to be
.Taking the signal amplitude in the ring to be 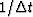 ,analogous to equation (8) the amplitude at time t is
,analogous to equation (8) the amplitude at time t is
| 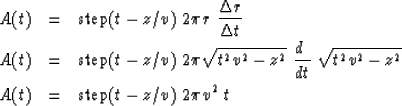 |
(9) |
| (10) |
| (11) |
As before, in seismology
we are interested in the high frequency behavior
so the scaling t in equation (11)
is not nearly so important as is the step function.
By equation (1)
the step function causes the spectrum to decay as 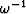 .Our original erroneous assumption
that Huygen's hyperbola of revolution
should carry a positive impulse
leads to the contradiction
that an impulsive plane wave
decomposed into Huygen's sources and added together again
does not preserve the constant spectrum
of the original impulsive waveform.
We can get the missing
.Our original erroneous assumption
that Huygen's hyperbola of revolution
should carry a positive impulse
leads to the contradiction
that an impulsive plane wave
decomposed into Huygen's sources and added together again
does not preserve the constant spectrum
of the original impulsive waveform.
We can get the missing 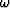 back into the spectrum
by having the hyperbola of revolution carry
a time-derivative filter instead of an impulse.
Thus in three dimensions,
a plane wave can be regarded, approximately,
as the superposition of many hyperboloidal responses,
each carrying a d/dt waveform.
back into the spectrum
by having the hyperbola of revolution carry
a time-derivative filter instead of an impulse.
Thus in three dimensions,
a plane wave can be regarded, approximately,
as the superposition of many hyperboloidal responses,
each carrying a d/dt waveform.





Next: About this document ...
Up: Claerbout: Hankel tail
Previous: HUYGEN'S SECONDARY SOURCE IN
Stanford Exploration Project
11/17/1997