Parameter sensitivity of the AVO coefficient

In this section we demonstrate the sensitivity of the AVO coefficient derived from the vertical and radial particle motion to variations in P-wave and S-wave velocity. As before, one of the velocities was varied by $\pm$ 100 m/s, while the other was kept constant. A similar study has been performed by Amundsen and Reitan Amundsen and Reitan (1994).

Figure 4 shows the sensitivity of the AVO coefficient to variations in the P-wave velocity. There is a significant sensitivity to changes in v_p at all angles of incidence. The higher the P-wave velocity, the smaller the angle at which the AVO coefficient reaches its minimum value of zero and the smaller the critical angle (R=1).

In Figure 5 we show the sensitivity of the AVO coefficient to variations in the S-wave velocity. At post-critical angles of incidence, there is a significant sensitivity to changes in v_s. The higher the S-wave velocity the smaller the AVO coefficient. There is also a considerable dependence on the S-wave velocity at pre-critical angles of incidence. Close to the critical angle, however, the AVO coefficient barely changes with variations in the S-wave velocity. This is due to the fact that R is independent to v_s2 at the critical angle.

 

ref2p Figure 4 AVO coefficient for P velocity variations of 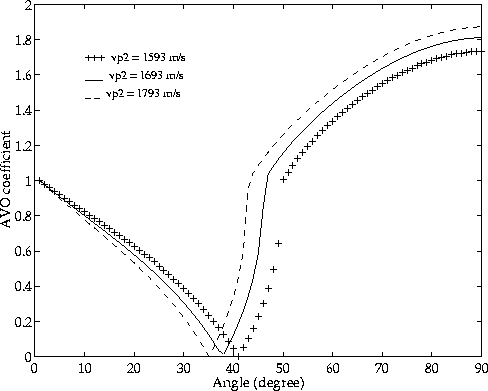$\pm$ 100 m/s.

 

ref2s Figure 5 AVO coefficient for S velocity variations of 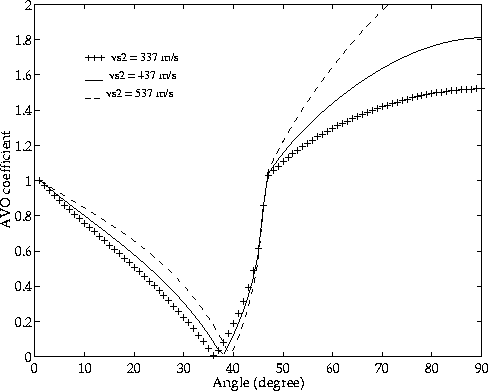$\pm$ 100 m/s.

Since the AVO coefficient is significantly sensitive to both P- and S-wave velocity before the critical angle, both parameters can be estimated for relatively small angles of incidence. However, it has to be taken into account that the radial velocity component will vanish at very small angles of incidence. Thus, the angular coverage should not be too small.