SEP-105 -- TABLE OF CONTENTS

Filtering & Optimization

Applications of plane-wave destructor filters (ps.gz 1758K) (pdf 9612K) (src 4673K)
Fomel S.
On several synthetic and real-data examples, I show that finite-difference plane-wave destructor filters can be a valuable alternative to prediction-error filters in applications such as data interpolation, fault detection, and noise attenuation.
Coherent noise attenuation using Inverse Problems and Prediction Error Filters (ps.gz 1034K) (pdf 3915K) (src 2579K)
Guitton A.
Two iterative methods that handle coherent noise effects during the inversion of 2-D prestack data are tested. One method approximates the inverse covariance matrices with PEFs, and the other introduces a coherent noise modeling operator in the objective function. This noise modeling operator is a PEF that has to be estimated before the inversion from a noise model or directly from the data. These two methods lead to Independent, Identically Distributed (IID) residual variables, thus guaranteeing a stable convergence of the inversion schemes and permitting coherent noise filtering/separation.
Two strategies for sparse data interpolation (ps.gz 1310K) (pdf 26862K) (src 6193K)
Brown M.
I introduce two strategies to overcome the slow convergence of least squares sparse data interpolation: 1) a 2-D multiscale Laplacian regularization operator, and 2) an explicit quadtree-style upsampling scheme which produces a good initial guess for iterative schemes. The multiscale regularization produces an order-of-magnitude speedup in the interpolation of a sparsely sampled topographical map. The quadtree method produces an initial guess which leads to similar speedups for iterative methods.
Multiple realizations using standard inversion techniques (ps.gz 998K) (pdf 7121K) (src 4220K)
Clapp R. G.
When solving a missing data problem, geophysicists and geostatisticians have very similar strategies. Each use the known data to characterize the model's covariance. At SEP we often characterize the covariance through Prediction Error Filters (PEFs) Claerbout (1999). Geostatisticians build variograms from the known data to represent the model's covariance Isaaks and Srivastava (1989). Once each has some measure of the model covariance they attempt to fill ...
Inverse B-spline interpolation (ps.gz 1783K) (pdf 13109K) (src 15269K)
Fomel S.
B-splines provide an accurate and efficient method for interpolating regularly spaced data. In this paper, I study the applicability of B-spline interpolation in the context of the inverse interpolation method for regularizing irregular data. Numerical tests show that, in comparison with lower-order linear interpolation, B-splines lead to a faster iterative conversion in under-determined problems and a more accurate result in over-determined problems. In addition, they provide a constructive method for creating discrete regularization operators from continuous differential equations.
3-D steering filters (ps.gz 497K) (pdf 4022K) (src 1488K)
Clapp R. G.
In recent reports I introduced the concept of a steering filter Clapp et al. (1997). Since then it has been used to regularize a wide variety of geophysical problems including interpolation Crawley (2000), multiple attenuation Clapp and Brown (1999, 2000), missing data problems Clapp et al. (1997), ...
Test case for PEF estimation with sparse data II (ps.gz 44K) (pdf 1995K) (src 58K)
Brown M., Claerbout J., and Fomel S.
The two-stage missing data interpolation approach of Claerbout (1999) (henceforth, the GEE approach) has been applied with great success Clapp et al. (1998); Crawley (2000); Fomel et al. (1997) in the past. The main strength of the approach lies in the ability of the prediction error filter (PEF) to find multiple, hidden correlation in the known data, and then, via regularization, to impose ...

Imaging

Tau tomography with steering filters: 3-D field data example, preliminary result (ps.gz 2007K) (pdf 11712K) (src 15986K)
Clapp R. G.
I extend tau tomography into 3-D. I apply steering filter regularized tau tomography on a 3-D North Sea Dataset. Early results show promise.
A tutorial on mixed-domain wave-equation migration and migration velocity analysis (ps.gz 571K) (pdf 6742K) (src 1016K)
Sava P.
This tutorial describes mixed-domain wave-equation migration and migration velocity analysis techniques in a unified theoretical framework. I review two of the most general mixed-domain migration methods, Fourier finite-difference and generalized screen, and show how other commonly used wave-equation migration methods come about as special cases. I use the Born approximation to derive general expressions for the wave-equation migration velocity analysis operator, and show two simple backprojection examples built around a North Sea dataset.
Simple factorization of implicit finite-difference downward-continuation operators (ps.gz 43K) (pdf 592K) (src 43K)
Biondi B.
Multi-dimensional Fourier transforms in the helical coordinate system (ps.gz 652K) (pdf 1515K) (src 3224K)
Rickett J. and Guitton A.
For every two-dimensional system with helical boundary conditions, there is an isomorphic one-dimensional system. Therefore, the one-dimensional FFT of a 2-D function wrapped on a helix is equivalent to a 2-D FFT. We show that the Fourier dual of helical boundary conditions is helical boundary conditions but with axes transposed, and we explicitly link the wavenumber vector, 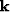${<B>k}$, in a multi-dimensional system with the wavenumber of a helical 1-D FFT, k_h. We illustrated the concepts with an example of multi-dimensional multiple prediction.
Seismic velocity and attribute study based on well interpolated data (ps.gz 1846K) (pdf 16509K) (src 6018K)
Gratwick D. and Rosales D.
This paper studies the effects of fluid type in pore space for a channel sand in the Stanford V dataset. The model used was created by interpolation of 3D well data using ordinary kriging. V_p, V_s, density, and porosity were all kriged into 3D volumes, and then a slice was extracted, which contained a sand body surrounded by a shale. Elastic modeling was run on this slice, and the data were processed into CMP gathers for AVO study. Subsequent modeling was done for fluid substitution of both oil and gas. It was found that the hydrocarbons yielded higher amplitude reflections, and that the gas model showed an increased amplitude with offset. A velocity slice containing well information was used for modeling and subsequent velocity analysis. This velocity analysis shows the difference between seismic and well velocities due to the frequency content of the source.
Amplitudes and inversion in the reflection angle domain (ps.gz 49K) (pdf 343K) (src 71K)
Prucha M. L. and Biondi B. L.
Reflection angle domain (RAD) imaging is gaining interest as an alternative to shot and offset domain methods Xu et al. (1998). The advantage of RAD imaging is that it reduces the number and strength of artifacts seen in complex areas, particularly artifacts caused by multipathing. RAD imaging reduces artifacts but does not overcome the inherent limitations in surface seismic recording geometries. As a result, areas where the RAD is most useful can also benefit from replacing migration with inversion. ...
Daylight imaging in V(x,y,z) media (ps.gz 278K) (pdf 1405K) (src 2280K)
Schuster G. T. and Rickett J.
Previous authors have tried to image seismic reflectivity by crosscorrelating passive seismic data, and treating the resultant correlograms as active source seismograms. We provide a mathematical framework for working with passive seismic correlograms that is both appropriate for V(x,y,z) media, and arbitrary source location. Under this framework, correlograms can be migrated with an imaging condition that is tuned to image particular events. For example, tuning the imaging condition to the kinematics of the Direct-Direct correlation event allows direct imaging of the seismic sources. Similarly, tuning to the Direct-Ghost correlation event allows imaging of subsurface reflectivity. Numerical results with synthetic data partly verify the effectiveness of crosscorrelation migration, but also suggest worse resolution of the image compared to standard Kirchhoff migration.