SEP-100 -- TABLE OF CONTENTS

Velocity

Everything depends on V(x,y,z) (ps.gz 734K) (pdf 531K) (src 702K)
Claerbout J.
Estimating 3-D velocity V(x,y,z) is the most important problem in exploration geophysics. It is a very difficult problem. In order to really solve it, SEP has turned to fundamentals of estimation theory with topographic data, regridding, interpolation, truncation, erratic noise, instrument drift, etc. This return to fundamentals has proven rewarding, leading us to the helix discovery. This discovery is revitalizing wave equation migration in 3-D, preconditioning many estimations (big speed up), and regularizing velocity estimation (blends measured and prior information). To enable young people to become productive with 3-D seismic data, Biondo Biondi and Bob Clapp have built a 3-D seismic software infrastructure that is able to address real 3-D problems, such as V(x,y,z) and aliasing in 3-D. This infrastructure is unique in the academic world. None of the other academic organizations have enough computing power and infrastructure to allow routine research activities with 3-D field data.
Wave-equation migration velocity analysis (ps.gz 1418K) (pdf 11489K) (src 32494K)
Biondi B. and Sava P.
In this report, we introduce a new wave-equation method of migration velocity analysis (MVA). The method is based on the linear relation that can be established between a perturbation in the migrated image and the generating perturbation in the slowness function. Our method consists of two steps: we first improve the focusing of the migrated image and then iteratively update the velocity model to explain the improvement in the focusing of the image. As a wave-equation method, our version of MVA is robust and generates smooth slowness functions without model regularization. We also show that our method has the potential to exploit the power of residual prestack migration to MVA.
Preconditioning tau tomography with geologic constraints (ps.gz 1443K) (pdf 5017K) (src 4352K)
Clapp R. G. and Biondi B.
Seismic tomography is a non-linear problem with a significant null-space. Our estimation problem often converges slowly, to a geologically unreasonable model, or not at all. One reason for slow or non-convergence is that we are attempting to simultaneously estimate reflector position (mapping velocity) and image our data (focusiing velocity). By performing tomography in vertical travel-time space, we avoid estimating mapping velocity, instead concentrating on focusing velocity. By introducing anisotropic preconditioning oriented along bedding planes, we can quickly guide the inversion towards a geologically reasonable model. We illustrate the benefits of our tomography method by comparing it to more traditional methods on a synthetic anticline model. In addition, we demonstrate the method's ability to improve the velocity estimate, and the resulting migrated image of a real 2-D dataset.
Why tau tomography is better than depth tomography (ps.gz 117K) (pdf 2318K) (src 779K)
Clapp R. G. and Biondi B.
Seismic tomography is a non-linear problem. A standard technique is to itteratively assume a linear relation between the change in slowness and the change in travel times Biondi (1990); Etgen (1990) and then re-linearize around the new model. In ray-based methods, this amounts to assuming stationary ray paths and reflection locations to construct a back projection ...
Velocity continuation in migration velocity analysis (ps.gz 1619K) (pdf 6105K) (src 4199K)
Fomel S.
Velocity continuation can be applied to migration velocity analysis. It enhances residual NMO correction by properly taking into account both vertical and lateral movements of reflectors caused by the change in migration velocity. I exemplify this fact with simple data tests.
All stationary points of differential semblance are asymptotic global minimizers: layered acoustics (ps.gz 137K) (pdf 676K) (src 583K)
Symes W. W.
Differential semblance velocity estimators have well-defined and smooth high frequency asymptotics. A version appropriate for analysis of CMP gathers and layered acoustic models has no secondary minima. Its structure suggests an approach to optimal parametrization of velocity models.
Coherent noise suppression in velocity inversion (ps.gz 245K) (pdf 4070K) (src 240K)
Symes W. W.
Data components with well-defined moveout other than primary reflections are sometimes called coherent noise. Coherent noise makes velocity analysis ambiguous, since no single velocity function explains incompatible moveouts simultaneously. Contemporary data processing treats the control of coherent noise influence on velocity as an interpretive step. Dual regularization theory suggests an alternative, automatic inversion algorithm for suppression of coherent noise when primary reflection phases dominate the data. Experiments with marine data illustrate the robustness and effectiveness of the algorithm.

Imaging

Angle-domain common image gathers by wave-equation migration (ps.gz 817K) (pdf 2210K) (src 2237K)
Prucha M. L., Biondi B. L., and Symes W. W.
Shot- and offset-domain common image gathers encounter problems in complex media. They can place events that come from different points in the subsurface at one subsurface location based on identical arrival times and horizontal slownesses. Angle-domain common image gathers uniquely define ray couples for each point in the subsurface, therefore each event in the data will be associated with only one subsurface location. It is possible to generate angle-domain common image gathers with wave-equation migration methods and these angle-domain common image gathers may be used for velocity analysis and amplitude-versus-angle analysis. Applications of these methods to the Marmousi model are promising.
Subsalt imaging by common-azimuth migration (ps.gz 507K) (pdf 6189K) (src 1728K)
Biondi B.
The comparison of subsalt images obtained by common-azimuth migration and single-arrival Kirchhoff migration demonstrates the potential of wave-equation migration when the velocity model causes complex multipathing. Subsalt reflectors are better imaged and the typical Kirchhoff artifacts caused by severe multipathing disappear. A detailed analysis of common-azimuth images indicates that the results of common-azimuth imaging could be improved. It points to opportunities to improve the numerical implementation as well as the downward continuation method.
Extending common-azimuth migration (ps.gz 253K) (pdf 843K) (src 309K)
Vaillant L. and Biondi B.
We present a review of common-azimuth prestack depth migration theory and propose a new extension to the original method. In common-azimuth migration theory, source and receiver raypaths are constrained to lie on the same plane at each depth level. By using data with a broader range of cross-line offsets, we increase the number of raypaths examined and consider more information. Consequently, our extended common-azimuth migration is theoretically better able to model lateral velocity variations due to real
3-D structures and is more compatible with the standard marine acquisition geometry, in which cross-line offsets are concentrated in a narrow band. We first discuss the theory of the process, and then introduce computational issues leading to future implementation.
Comparing Kirchhoff with wave equation migration in a hydrate region (ps.gz 1181K) (pdf 4343K) (src 1236K)
Sinha M. and Biondi B.
Prestack migration is necessary before AVO analysis. Most of the present migration algorithms not only try to focus the reflections on the subsurface but also strive to preserve the amplitude for subsequent amplitude studies. A migration/inversion method developed by Lumley 1993 estimates the angle dependent reflectivity at each subsurface point by using least-squares Kirchhoff migration followed by a linearized Zoeppritz elastic parameter inversion for relative contrasts in compressional and shear wave impedance. Another migration algorithm is based on the wave-equation method which uses the Double ...
Angle-gather time migration (ps.gz 1296K) (pdf 5089K) (src 1674K)
Fomel S. and Prucha M.
Angle-gather migration creates seismic images for different reflection angles at the reflector. We formulate an angle-gather time migration algorithm and study its properties. The algorithm serves as an educational introduction to the angle gather concept. It also looks attractive as a practical alternative to conventional common-offset time migration both for velocity analysis and for AVO/AVA analysis.
On Stolt prestack residual migration (ps.gz 1440K) (pdf 4196K) (src 91891K)
Sava P.
Residual migration has proved to be a useful tool in imaging and in velocity analysis. Rothman 1983 shows that post-stack residual migration can be successfully used to improve the focusing of the migrated sections. He also showed that migration with a given velocity v_m is equivalent to migration with a reference velocity v₀ followed by residual migration with a velocity v_r that can be expressed as a function of v₀ and v_m. ...
Anti-aliasing multiple prediction beyond two dimensions (ps.gz 166K) (pdf 4268K) (src 19192K)
Sun Y.
Theoretically, the Delft method of surface-related multiple elimination can be applied in three dimensions, as long as the source and receiver coverage is dense enough. In reality, such a dense coverage is still far from reach, using the available multi-streamer acquisition system. One way to fill the gap is to massively interpolate the missing sources and receivers in the survey, which requires a huge computational cost. In this paper, I propose a more practical approach for the multi-streamer system. Instead of using large-volume missing-streamer interpolation, my method finds the most reasonable proxy from the collected dataset for each missing trace needed in the multiple prediction. Although this approach avoids missing-streamer interpolation, another problem pops up in the multi-streamer case, the aliasing noise caused by the sparse sampling in the cross-line direction. To solve this problem, I introduce a new concept, the partially-stacked multiple contribution gather (PSMCG). Using multi-scale prediction-error filter (MSPEF) theory, this approach interpolates the PSMCG in the cross-line direction to remove the aliasing noise.

Helix filtering

Acoustic daylight imaging via spectral factorization: Helioseismology and reservoir monitoring (ps.gz 465K) (pdf 762K) (src 1761K)
Rickett J. and Claerbout J.
The acoustic time history of the sun's surface is a stochastic (t,x,y)-cube of information. Helioseismologists cross-correlate these noise traces to produce impulse response seismograms, providing the proof of concept for a long-standing geophysical conjecture. We pack the (x,y)-mesh of time series into a single super-long one-dimensional time series. We apply Kolmogoroff spectral factorization to the super-trace, unpack, and find the multidimensional acoustic impulse response of the sun. State-of-the-art seismic exploration recording equipment offers tens of thousands of channels, and permanent recording installations are becoming economically realistic. Helioseismology, therefore, provides a conceptual prototype for using natural noises for continuous reservoir monitoring.
Interpolation with smoothly nonstationary prediction-error filters (ps.gz 723K) (pdf 3470K) (src 2376K)
Crawley S.
Building on the notions of time-variable filtering and the helix coordinate system, I develop software for filters that are smoothly variable in multiple dimensions, but that are quantized into large enough regions to be efficient. Multiscale prediction-error filters (PEFs) can estimate dips from recorded data and use the dip information to fill in unrecorded shot or receiver gathers. The data are typically divided into patches with approximately constant dips, with the requirement that the patches contain enough data samples to provide a sufficient number of fitting equations to determine all the coefficients of the filter. Each patch of data represents an independent estimation problem. Instead, I estimate a set of smoothly varying filters in much smaller patches, as small as one data sample. They are more work to estimate, but the smoothly varying filters do give more accurate interpolation results than PEFs in independent patches, particularly on complicated data. To control the smoothness of the filters. I use filters like directional derivatives that Clapp et al. 1998 call ``steering filters''. They destroy dips in easily adjusted directions. I use them in residual space to encourage dips in the specified directions. I describe the notion of ``radial-steering filters'' Clapp et al. (1999), i.e., steering filters oriented in the radial direction (lines of constant x/t in (t,x) space). Break a common-midpoint gather into pie shaped regions bounded by various values of x/t. Such a pie-shaped region tends to have constant dip spectrum throughout the region so it is a natural region for smoothing estimates of dip spectra or of gathering statistics (via 2-D PEFs). In this paper I use smoothly variable PEFs to interpolate missing traces, though they may have many other uses. Finally, since noisy data can produce poor interpolation results, I deal with the separation of signal and noise along with missing data.
Directional smoothing of non-stationary filters (ps.gz 664K) (pdf 2384K) (src 5961K)
Clapp R. G., Fomel S., Crawley S., and Claerbout J. F.
Space-varying prediction error filters are an effective tool in solving a number of common geophysical problems. To estimate these filters some type of regularization is necessary. An effective method is to smooth the filters along radial lines in CMP gathers where dip information is relatively unchanging.
Texture synthesis and prediction error filtering (ps.gz 695K) (pdf 2155K) (src 1982K)
Brown M.
The spectrum of a prediction-error filter (PEF) tends toward the inverse spectrum of the data from which it is estimated. I compute 2-D PEF's from known ``training images'' and use them to synthesize similar-looking textures from random numbers via helix deconvolution. Compared to a similar technique employing Fourier transforms, the PEF-based method is generally more flexible, due to its ability to handle missing data, a fact which I illustrate with an example. Applying PEF-based texture synthesis to a stacked 2-D seismic section, I note that the residual error in the PEF estimation forms the basis for ``coherency'' analysis by highlighting discontinuities in the data, and may also serve as a measure of the quality of a given migration velocity model. Last, I relate the notion of texture synthesis to missing data interpolation and show an example.
Polarity and PEF regularization (ps.gz 692K) (pdf 1327K) (src 759K)
Claerbout J.
We address the puzzle of seismic polarity. Why do we rarely observe it clearly and how could we be more systematic about trying to observe polarity? This puzzle will lead us to long prediction-error filters. Being long, they require many data samples. If such a filter is nonstationary, we might have an inadequate number of fitting equations. Then we need regularization. Here we consider some examples and consider an efficient way to regularize the filter estimation. ...
Spectral factorization revisited (ps.gz 96K) (pdf 491K) (src 20K)
Sava P. and Fomel S.
In this paper, we review some of the iterative methods for the square root, showing that all these methods belong to the same family, for which we find a general formula. We then explain how those iterative methods for real numbers can be extended to spectral factorization of auto-correlations. The iteration based on the Newton-Raphson method is optimal from the convergence stand point, though it is not optimal as far as stability is concerned. Finally, we show that other members of the iteration family are more stable, though slightly more expensive and slower to converge.
Helix derivative and low-cut filters' spectral feature and application (ps.gz 7788K) (pdf 20583K) (src 14988K)
Zhao Y.
A helix derivative filter can be used to roughen an image and thus enhance its details. Unlike the conventional derivative operator, the helix derivative filter has no direction orientation. I present the enhanced helix/low-cut derivative filters, in which the zero frequency response is adjustable. I analyze the quantitative effects of the adjustable parameters on the filter spectrum and propose guidelines for choosing parameters. I also show some roughened images created by the enhanced filters.
Helical meshes on spheres and cones (ps.gz 148K) (pdf 1089K) (src 389K)
Claerbout J.
We embed a helix in the two-dimensional surface of a sphere; likewise, in the two-dimensional surface of a cone. This provides a one-dimensional coordinate system on a two-dimensional surface. Although mesh points are exactly evenly spaced along the helix and approximately evenly spaced in the crossline dimension, unfortunately, the angles between neighboring points are continuously changing. We seem to lose the concepts of two-dimensional autoregression that we have in cartesian space.

Traveltimes

3-D traveltime computation by Huygens wavefront tracing (ps.gz 785K) (pdf 9670K) (src 3988K)
Sava P.
In this paper, I present a 3-D implementation of Huygens wavefront tracing. The three-dimensional version of the method retains the characteristics of the two-dimensional one: stability, accuracy, and efficiency. The major difficulty of the 3-D extension is related to the handling of triplications. An easy to implement solution is to approximate the wavefronts at the triplications as planes orthogonal to the incident ray.
An adaptive finite difference method for traveltime and amplitude (ps.gz 272K) (pdf 2421K) (src 196K)
Qian J. and Symes W. W.
The eikonal equation with point source is difficult to solve with high order accuracy because of the singularity of the solution at the source. All the formally high order schemes turn out to be first order accurate without special treatment of this singularity. Adaptive upwind finite difference methods based on high order ENO (Essentially NonOscillatory) Runge-Kutta difference schemes for the paraxial eikonal equation overcome this difficulty. The method controls error by automatic grid refinement and coarsening based on an a posteriori error estimation. It achieves prescribed accuracy at far lower cost than fixed grid methods. Reliable auxiliary quantities, such as take-off angle and geometrical spreading factor, are by-products.
A second-order fast marching eikonal solver (ps.gz 189K) (pdf 1379K) (src 618K)
Rickett J. and Fomel S.
The fast marching method Sethian (1996) is widely used for solving the eikonal equation in Cartesian coordinates. The method's principal advantages are: stability, computational efficiency, and algorithmic simplicity. Within geophysics, fast marching traveltime calculations Popovici and Sethian (1997) may be used for 3-D depth migration or velocity analysis. ...

Optimization

Robust and stable velocity analysis using the Huber function (ps.gz 1514K) (pdf 9015K) (src 3949K)
Guitton A. and Symes W. W.
The Huber function is one of several robust error measures which interpolates between smooth (l²) treatment of small residuals and robust (l¹) treatment of large residuals. Since the Huber function is differentiable, it may be minimized reliably with a standard gradient-based optimizer. Tests with a linear inverse problem for velocity analysis, using both synthetic and field data, suggest that (1) the Huber function gives far more robust model estimates than does least squares, (2) its minimization using a standard quasi-Newton method is comparable in computational cost to least squares estimation using conjugate gradient iteration, and (3) the result of Huber data fitting is stable over a wide range of choices for 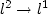$l^2 l^1$ threshold and total number of quasi-Newton steps.
Extremal regularization (ps.gz 112K) (pdf 1396K) (src 967K)
Symes W. W.
Extremal regularization finds a model fitting the data to a specified tolerance, and additionally minimizing an auxiliary criterion. It provides relative model/data space weights when no statistical information about the model or data is available other than an estimate of noise level. A version of the Moré-Hebden algorithm using conjugate gradients to solve the various linear systems implements extremal regularization for large scale inverse problems. A deconvolution application illustrates the possibilities and pitfalls of extremal regularization in the linear case.

Reservoir Characterization

Backus revisited: Just in time (ps.gz 71K) (pdf 45K) (src 2K)
Muir F.
The essence of Backus theory Backus (1962) is that it allows a bunch of layers to be replaced by a single layer. The new homogeneous medium has elastic properties identical in the long-wavelength limit so that mass and travel-time are conserved, but wavelet shape is not. In this paper I show that for normal incidence plane waves the three elastic layer parameters of thickness, compliance, and density can be replaced by the two, travel-time and impedance, without losing reflection and transmission ...
Elastic wave propagation and attenuation in a double-porosity dual-permeability medium (ps.gz 125K) (pdf 1154K) (src 38K)
Berryman J. G. and Wang H. F.
To account for large-volume low-permeability storage porosity and low-volume high-permeability fracture/crack porosity in oil and gas reservoirs, phenomenological equations for the poroelastic behavior of a double porosity medium have been formulated and the coefficients in these linear equations identified. This generalization from a single porosity model increases the number of independent inertial coefficients from three to six, the number of independent drag coefficients from three to six, and the number of independent stress-strain coefficients from three to six for an isotropic applied stress and assumed isotropy of the medium. The analysis leading to physical interpretations of the inertial and drag coefficients is relatively straightforward, whereas that for the stress-strain coefficients is more tedious. In a quasistatic analysis, the physical interpretations are based upon considerations of extremes in both spatial and temporal scales. The limit of very short times is the one most pertinent for wave propagation, and in this case both matrix porosity and fractures are expected to behave in an undrained fashion, although our analysis makes no assumptions in this regard. For the very long times more relevant to reservoir drawdown, the double porosity medium behaves as an equivalent single porosity medium. At the macroscopic spatial level, the pertinent parameters (such as the total compressibility) may be determined by appropriate field tests. At the mesoscopic scale pertinent parameters of the rock matrix can be determined directly through laboratory measurements on core, and the compressiblity can be measured for a single fracture. We show explicitly how to generalize the quasistatic results to incorporate wave propagation effects and how effects that are usually attributed to squirt flow under partially saturated conditions can be explained alternatively in terms of the double-porosity model. The result is therefore a theory that generalizes, but is completely consistent with, Biot's theory of poroelasticity and is valid for analysis of elastic wave data from highly fractured reservoirs.

Anisotropy

A short tour through the Stanford Exploration Project contributions to anisotropy (ps.gz 33K) (pdf 75K) (src 6K)
Alkhalifah T.